Обозначим через F конечное подмножество вещественных чисел, с которыми оперирует ЭВМ. То есть элементы множества F – это вещественные числа, которые точно представимы в ЭВМ. Если f1, f2 – элементы множества F, ближайшие друг к другу, и x Î [f1,f2], где x – это число, не представимое точно в ЭВМ, то x равняется либо f1, либо f2.
Разность между истинным значением числа и его приближением на ЭВМ (т.е. элементом множества F) называется ошибкой округления на ЭВМ.
Если f1, f2 принадлежат F, то сумма этих чисел, разность, произведение и частное могут не принадлежать F.
Следует помнить, что многие числа не представимы точно в ЭВМ. Например, число 0.1 не представимо точно на любой ЭВМ, у которой основание системы счисления является степенью 2.
Точность вычислений с вещественными числами на ЭВМ можно оценить с помощью машинного e.
Машинным e называется наименьшее положительное вещественное число, такое что 1Åe >1, где Å – сложение на ЭВМ.
Если для представления вещественного числа в памяти ЭВМ
отводится 32 бита, то машинное e
приближенно равно 2×10-8 .
То есть в этом случае 
.
При сложении и вычитании на ЭВМ вещественных чисел, сильно отличающихся друг от друга по модулю, происходит потеря верных значащих цифр. При вычитании чисел одинакового знака и близких по модулю также происходит потеря верных значащих цифр. В плохо продуманных вычислительных алгоритмах за счет этого возможна катастрофическая потеря верных цифр.
Абсолютная погрешность суммы или разности нескольких приближенных чисел равна сумме абсолютных погрешностей слагаемых, т.е.:
, 
.
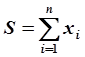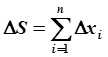Относительная погрешность суммы вычисляется по формуле: 
.
Пример
Даны приближенные числа a = 0.01234 и b = 0.01231 и их абсолютные погрешности Da = 0.000002, Db = 0.000002, найти абсолютную и относительную погрешности разности чисел.
M = a – b, M = 0.00003, DM = Da + Db = 0.000004,
.
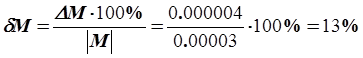Отметим, что числа a и b содержат по четыре верные значащие цифры:
а = 0.01234, b = 0.01231,
Da = 0.000002, Db = 0.01231, а разность этих чисел М содержит только одну верную значащую цифру:
M = 0.00003,
DM = 0.000004.
Произошла потеря верных значащих цифр. Относительная погрешность чисел a и b мала (da = 0.016 %, db = 0.016 %), а относительная погрешность разности велика (dM = 13 %).
При умножении и делении приближенных чисел относительная погрешность результата равна сумме относительных погрешностей чисел:
, 
.
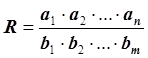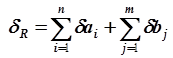Абсолютная погрешность степенной функции y = xm, где x – приближенное положительное число, равна
.
Относительная погрешность степенной функции y = xm равна: 
.
Пример
Относительная погрешность квадрата x2 вдвое больше относительной
погрешности x, относительная
погрешность квадратного корня 
вдвое меньше относительной
погрешности числа x,
относительная погрешность обратной величины 1/x
равна относительной погрешности числа x.
Абсолютная погрешность дифференцируемой функции y = f(x), вызываемая достаточно малой погрешностью
аргумента Dx, оценивается величиной :
.
Если значения функции f(x) положительны, то для относительной погрешности имеет место оценка:
.
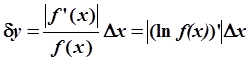Пример 1
Абсолютные погрешности синуса и косинуса находится по формулам:
D sin x = |cos x|×Dx,
D cos x = |sin x|×Dx, где x изменяется в радианах.
Погрешность вычисления значения функции нескольких переменных (общая формула для погрешности)
Абсолютная погрешность дифференцируемой функции y = f(x1, x2, x3, …, xn), вызываемая достаточно малыми погрешностями Dx1, Dx2,…,Dxn аргументов x1, x2, x3,…,xn, оценивается величиной:
.
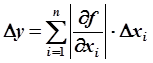Пример 2
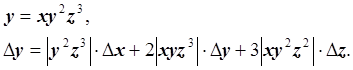
Если значения функции положительны, то для относительной погрешности имеет место оценка:
.
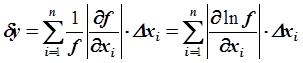Пример 3
Вычислить значение функции f, абсолютную и относительную погрешности вычисления f, если
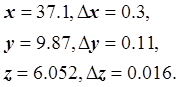
Сначала найдем относительную погрешность вычисления значения f, а затем абсолютную погрешность. Функция f положительна и дифференцируема, поэтому воспользуемся формулой:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.