Вычислительная математика как часть математики, страница 7

Построить алгоритм для уточнения коря уравнения x³ + 3x – 1 = 0 на отрезке [0,1] методом Ньютона с точностью e.

Решение

1. Отрезок [0, 1] содержит один корень уравнения f(x) = 0. Функция f(x) является дважды непрерывно дифференцируемой на отрезке [0, 1] (f(x) Î C²[0, 1]). Функция f принимает на концах отрезка [0, 1] значения разных знаков. Первая производная функция f не обращаются в ноль на отрезке. То есть:

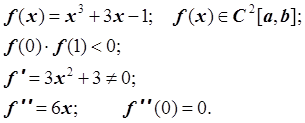
Вторая производная f обращается в ноль на отрезке [0, 1]. В таких случаях рекомендуется уменьшить отрезок [a, b] таким образом, чтобы уменьшенный отрезок содержал корень уравнения, и для этого отрезка выполнялись все условия.

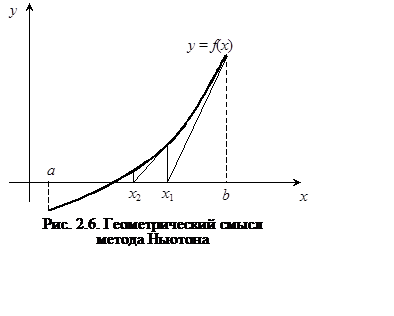Рассмотрим отрезок  [0.1, 1].  Этот  отрезок  содержит  один  корень уравнения f(x) = 0 и для него выполняются все условия для функции f(x).

2. Формула метода:

.

3. f(1) f ¢¢(x) > 0, начальное приближение  x₀ = 1.

4. Условие остановки итерационного процесса:

.

Число x_n+1, для которого выполняется условие остановки, является приближенным значением корня уравнения на отрезке [0.1, 1], найденным методом Ньютона с точностью e. На рис. 2.6. иллюстрируется применение метода Ньютона. В рассматриваемом случае начальное приближение x₀ = b. Метод Ньютона называют также методом касательных.

2.6. Метод хорд

1. Условия на применение метода хорд те же самые, что и для метода Ньютона.

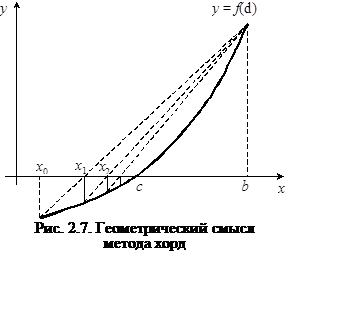
Пусть известен отрезок [a, b], который содержит один корень уравнения f(x) = 0.  Функция f(x) является дважды непрерывно дифференцируемой на [a, b](f(x) Î C²[a,b]). Функция f принимает на концах отрезка [a, b] значения разных знаков (f(a)×f(b) < 0). Первая  и вторая  производные  функции  f  не обращаются в ноль на отрезке [a, b] (f ¢ ¹ 0, f ¢¢ ¹ 0). При выполнении этих условий для уточнения корня можно использовать метод хорд.

2. Формула метода: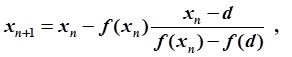  

то есть 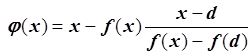                                    , где d – неподвижная точка, которая выбирается из условия f(d)×f ¢¢ (x) > 0. То есть условие на начальное приближение в методе Ньютона соответствует условию на неподвижную точку в методе хорд:

если f(a)×f ¢¢ (x) > 0,        то d = a;

если f(b)×f ¢¢ (x) > 0,        то d =b.

3.    Если d = a,             то начальное приближение x₀ = b.

Если d = b,             то начальное приближение x₀ = a.

Таким образом, один из концов отрезка является неподвижной точкой, а другой – точкой начального приближения.

4. Условие остановки итерационного процесса то же самое, что и для метода Ньютона:

, где .

При выполнении этого условия x_n+1является приближенным значением корня уравненияf(x) = 0 на отрезке [a, b], найденным методом хорд с точностью e.  На рис. 2.7. иллюстрируется применение метода хорд, в рассматриваемом случае неподвижная точка d = b.

Пример

Построить алгоритм для уточнения корня уравнения x³ + 3x – 1 = 0 на отрезке [0,1] методом хорд с точностью e.

Решение

f(x) =  x³ + 3 x- 1.

1. В предыдущем примере мы убедились, что от отрезка [0, 1] нужно перейти к уменьшенному отрезку [0.1, 1]. Этот отрезок содержит один корень уравнения f(x) = 0 и для него выполняются все условия для функции f.

2. , следовательно, d = 1.

Формула метода: .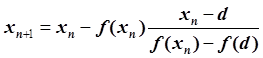

3. Так как d = 1, начальное приближение x₀ = 0.1.

4. Условие остановки итерационного процесса:

, где .

Число x_n+1, для которого выполняется условие остановки итерационного процесса, является приближенным значением корня уравнения f(x) = 0 на отрезке [0,1, 1], найденным методом хорд с точностью e.

2.7. Комбинированный метод хорд и касательных

Метод Ньютона называют также методом касательных. Комбинируя метод хорд и метод Ньютона, можно построить метод отыскания вещественных корней уравнения f(x) = 0, в котором при прежних предположениях относительно f(x) на каждом шаге итерационного процесса мы получаем  два приближения к корню  и  , причем  где с –точное значение корня.

1. Условия на применение метода те же, что и в методе Ньютона.

Пусть известен отрезок [a, b], который содержит один корень уравнения: f(x) = 0. Функция f(x) является дважды непрерывно дифференцируемой на [a, b](f(x) Î C²[a, b]). Функция f принимает на концах отрезка [a, b] значения разных знаков (f(a)×f(b) < 0). Первая  и  вторая  производные  функции  f  не  обращаются  в  ноль  на отрезке [a, b]