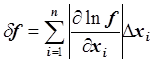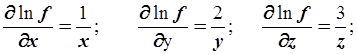
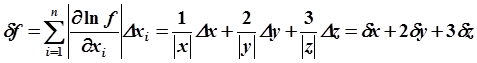Вычислительная математика как часть математики, страница 4

;       ;

;

.

Найдем относительные погрешности аргументов:

; .

Относительная погрешность является величиной порядка 1 %, следовательно, значение f содержит 2 верные значащие цифры. Следовательно, в записи f  нужно указать три значащие цифры, две из которых будут верными  и одна сомнительная. Вычислим xy²z³ = 801133.57, оставляя три значащие цифры, получим: f = 801*10³. Зная значение f и её относительную погрешность, найдем абсолютную погрешность:

.

1.7. Примеры решения задач

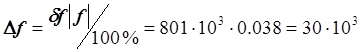Задача 1

Число x = 12.371содержит 3 верные значащие цифры, определить, какова относительная погрешность этого числа.

Решение

По определению верной значащей цифры

12.371,               Dx = 0.05,       .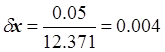

Отметим, что в данной задаче абсолютная погрешность Dx для любого x представляется в виде 5×10ⁿ, где значение n зависит от числа верных значащих цифр.

Ответ:  dx = 0.004  (либо dx = 0.4%).

Задача 2

Определить сколько верных значащих цифр содержит число x = 1.415, если относительная погрешность этого числа составляет 1%.

Решение

Сначала, зная x и его относительную погрешность, найдём абсолютную погрешность, а затем по определению верных значащих цифр найдём их количество:

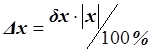x     = 1.415, , следовательно  , Δx = 0.01.

x     = 1.415.

Dx   = 0.01, следовательно число x содержит две верные значащие цифры.

Ответ: число x содержит две верные значащие цифры (1, 4).

Задача 3

Даны числа a и b с абсолютными погрешностями  Da и Db. Найти относительные погрешности суммы, разности, частного и произведения этих чисел.

Дано:

a = 2.35;  Da = 0.01;

b = 3.41; Db = 0.02;

S = a + b; M = a – b; P = ab; Q = a/b.

Найти: d_S, d_M, d_P, d_Q.

Решение

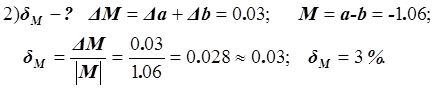
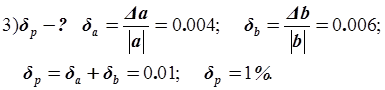
Ответ:

Задача 4

Найти абсолютную и относительную погрешность вычисления значения функцииf:

,          

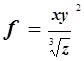Решение

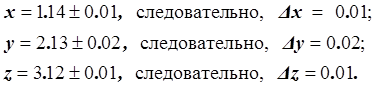
Сначала найдем относительную погрешность вычисления значения f, а затем абсолютную погрешность. Функция f положительна и дифференцируема, поэтому воспользуемся формулой:

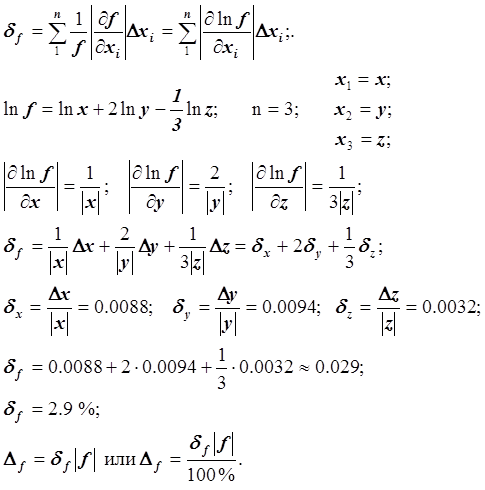
Так как , то значение функции f содержит 2 верных знака. Вычисляем  и записываем   (число содержит две верные значащие цифры и одну сомнительную).

.

Ответ: .

2. Численные методы решения нелинейных уравнений

Рассмотрим уравнение: f(x) = 0. В дальнейшем мы будем говорить только о вещественных корнях этого уравнения.

Рекомендуемая литература: /2-6, 12-13/.

2.1. Постановка задачи

Пусть уравнение f(x) = 0 имеет k вещественных корней c₁,c₂,…,c_k. Требуется найти числа , такие, что , где e – заданная точность, 1 £ j £ k.

Задача нахождения приближенных значений корней разбивается на два этапа:

1) отделение корней;

2) уточнение корней с заданной точностью.

Этап отделения вещественных корней заключается в отыскании достаточно малых отрезков [a_j, b_j] таких, что каждый из этих отрезков содержит один корень уравнения (с_j Î [a_j, b_j], 1 £ j £ k) и каждый вещественный корень содержится ровно в одном отрезке.

На этапе уточнения корня известен отрезок [a, b], который содержит один корень уравнения  (с Î [a, b]). Ставится задача вычисления корня с заданной точностью, то есть нахождения  такого, что , где e – заданная точность.

2.2. Отделение корней

Рассматривается два способа решения задачи отделения корней – графический и аналитический.

Существует два подхода к графическому отделению корней.

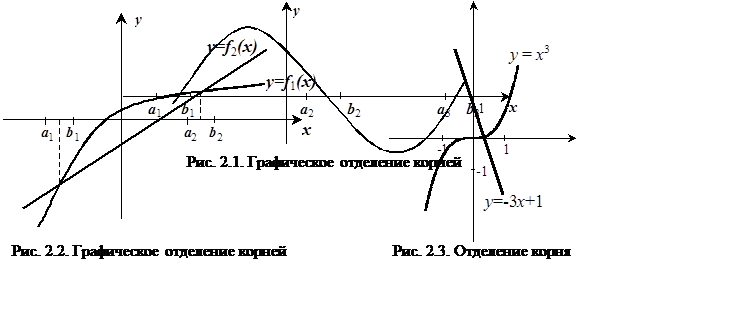
1. Строится график:  и приблизительно находятся абсциссы точек пересечения графика  с осью x (рис. 2.1).

2. Сначала уравнение  записывается в виде , а затем строятся графики:  и приблизительно находятся абсциссы точек пересечения этих графиков (рис. 2.2).

Пример

Требуется отделить корни уравнения: .

Решение. Запишем уравнение в виде: , то есть , , и построим графики:  (рис. 2.3). Абсцисса точки пересечения графиков принадлежит отрезку [0, 1].

Отрезок  [0, 1]  содержит один корень уравнения: .

Аналитически корни уравнения  можно отделить, используя свойства функции, например, опираясь на следующую теорему.

Теорема

Если f(x) = 0 является непрерывно дифференцируемой функцией на отрезке , первая производная f не меняет знак на [a, b] , и на концах отрезка функция f принимает значения разных знаков , то внутри отрезка [a, b] содержится один корень уравнения f(x) = 0.