Структурный, кинематический и динамический анализ кривошипно-ползунного механизма и шарнирного четырёхзвенника, страница 9

                                 (31)

В этом векторном уравнение неизвестны только величина и направление вектора . Реакцию  определяем графически, построением векторного многоугольника, замыкающим звеном которого будет вектор . Выбираем произвольно масштаб плана сил  и определяем отрезки векторов, изображающих эти силы на плане сил.

;    

;       

;        

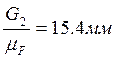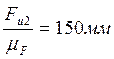
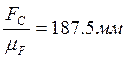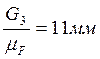
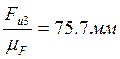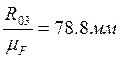
На чертеже выбираем произвольную точку «а» и последовательно откладываем векторы сил векторного уравнения. Величина R₀₃ в связи с её малостью пренебрегаем. Построение известных сил заканчивается в точке «b». Так как многоугольник сил, выражающий векторное уравнение , должен быть замкнутым, соединяем точку b и а прямой линией, изображающей в масштабе  реакцию . Её величина

Реакцию  в шарнирной опоре, соединяющей шатун и ползун, определим из уравнения равновесия шатуна

                                    (32)

Расчет ведущего звена

Вычерчиваем ведущее звено в произвольном масштабе (принимаем АВ=128 мм, т.е. ) в положении 9. Прикладываем все действующие на него силы: в точке  - силы  и ; в точке В – силу  перпендикулярно АВ, уравновешивающую силу, т.е. силу замещающую действие всего отброшенного механизма на ведущее звено, включая силу полезного сопротивления, и реакцию , взаимодействия 1-го звена-кривошипа и 2-го звена-шатуна в шарнирной опоре.

Уравновешивающую силу определим из условия равновесия ведущего звена составив уравнение равновесия – сумма моментов сил, действующих на ведущее звено, относительно точки А, равно нулю.

                                       (33)

откуда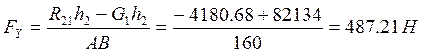

Здесь h₁ и h₂ – отрезки, измерены непосредственно на схеме звена 1.

Для определения реакции R₀₁ кривошипа и стойки в шарнирной опоре составляем уравнение равновесия звена 1 – геометрическая сумма сил, действующих на звено, равно нулю

                                        (34)

Строим план сил в масштабе .

;  ; 

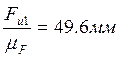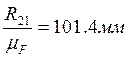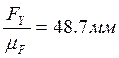
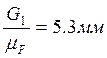
Соединив точки k и e, получаем вектор R₀₁,величина которого будет

1.3.4. Построение графика приведенных моментов сил сопротивления

Приведенный момент сил сопротивления представим в виде уравнения

                                                                         (35)

где  - приведенная сила равная по величине и противоположна по направлению уравновешивающей силы .

Определяем  уравновешивающую силу методом Жуковского.

Для этого к построенным планам скоростей в точке С прикладываем повёрнутую на 90º силу сопротивления F_C, а в точке В – перпендикулярно  АВ - уравновешивающую силу F_Y, направив её таким образом, чтобы создаваемый ею момент относительно полюса Р был противоположен по направлению моменту, создаваемому силой F_C.

Уравнение равновесия рычага Жуковского

 откуда, 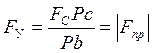                                   (36)

где Рс и Pb – отрезки, измеряемые непосредственно на планах скоростей.

Построение графика приведенных моментов сил сопротивления.

Для определения мощности на валу кривошипа необходимо определить фактический момент движущих сил М_Д, приложенный к ведущему валу (кривошипу). Момент движущих сил можно определить графическим, используя графики моментов сил сопротивления и работы сил сопротивления.

Для построения графика приведенных моментов сил сопротивления по формуле

Результаты вычислений сведены в табл. 7

Таблица 7

Расчет приведенного момента сил сопротивления