Структурный, кинематический и динамический анализ кривошипно-ползунного механизма и шарнирного четырёхзвенника, страница 2

 - количество двухподвижных кинематических пар четвертого класса.

Рассматриваемый механизм состоит из трёх подвижных звеньев, т.е. n = 3, содержит четыре кинематические пары пятого класса,, из которых одна является поступательной -соединяет ползун 3 со стойкой 0, и три – вращательные, В₀₁, - соединяет шарниром кривошип 1 со стойкой 0; пара В₁₂ – соединяет шарниром кривошип 1 с шатуном 2; пара В₂₃ – соединяет шарниром шатун 2 с ползуном 3.

Кинематических пар четвёртого класса в механизме нет, .

Степень подвижности механизма

Механизм состоит  из начального механизма, содержащего кривошип 1, стойку 0 и одну вращательную кинематическую пару В₀₁ (рис.3) и одной группы Асура, содержащей шатун 2, ползун 3 и три кинематические пары (рис. 4), вращательные В₁₂ и В₂₀ и поступательную П₃₀.

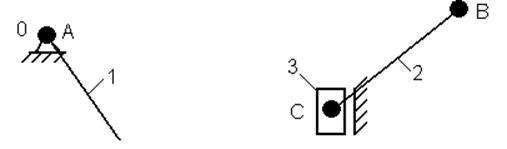
Рис. 3 Начальный механизм                                  Рис. 4 Группа Ассура

Формула строения механизма это последовательность присоединения к начальному механизму звеньев механизма .

Из структурного анализа механизма, что для получения вполне определенных движений звеньев, достаточно первоначально задать одному из звеньев определённое движение. Это и подтверждается принципом образования механизмов по Асуру. В нашем механизме задано вращательное  движение с постоянной угловой скоростью  шатуну .

1.2. КИНЕМАТИЧЕСКИЙ АНАЛИЗ МЕХАНИЗМА

Задачами кинематического анализа являются: определение траекторий движения точек звеньев, линейных скоростей и ускорений точек звеньев, угловых скоростей и ускорений звеньев. Эти задачи решаются путём построения планов положений механизма, скоростей и ускорений точек звеньев механизма и путём построения кинематических диаграмм.

1.2.1. Построение планов положений механизма

Для построения планов положений механизма необходимо выбрать масштаб длины.

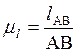                                                                                    (2)

где АВ – отрезок прямой, изображающий кривошип на чертеже.

Принимаем произвольно длину кривошипа на чертеже АВ = 60 мм, тогда

.

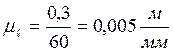Определяем масштабную длину ВС, изображающую длину шатуна .

.

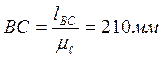Определяем масштабную длину смещения у.

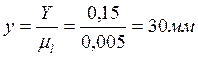
По принятой величине АВ и полученной ВС строем схему механизма в 12-ти положениях.

Изображаем известные траектории движения точек звеньев механизма. В нашем механизме известна траектория движения точки В кривошипа, это окружность с радиусом равным длине кривошипа , и прямолинейная траектория вдоль направляющей ползуна x-x. Из точки А проводим окружность радиусом АВ и делим её на 12 равных частей. Деление начинаем с положения, когда ползун находится крайней нижней точке, при этом кривошип и шатун вытягиваются в одну линию. Из точки А радиусом АВ+ВС проводим дугу, пересекая прямую x-x получим точку С₀. деление окружности на 12 частей проводим от крайней нижней точки В₀ по направлению вращения кривошипа. Из полученных точек   радиусом ВС проводим дуги на пересечении прямой x-x, получим точки  Второе крайнее положение ползуна определяем дугой радиуса (ВС-АВ) на направляющей x-x, обозначаем точку , номер точки – ближайший предыдущий номер.  соединим с точкой А до пересечения с окружностью, получим точку . Соединяем прямыми линиями точки  с соответствующими точками  и далее с точкой А. Во всех положениях шатуна АВ определим его середину и обозначим точки , соединим эти точки плавной кривой, что дает траекторию движения центра масс ползуна.

Таким образом, из построенных 12 планов положений механизма видно, что траектории движения точек: В-окружность радиусом АВ: С – прямо по Х-Х: S (центр масс шатуна) - шатунная кривая. Ход ползуна

;

где  - расстояние между крайними точками расположения ползуна на плане положения механизма,

1.2.2 Определение скоростей точек звеньев механизма с помощью планов скоростей

Определяем скорость точки В, совершающей равномерное вращательное движение

                                                                          (3)