Структурный, кинематический и динамический анализ кривошипно-ползунного механизма и шарнирного четырёхзвенника, страница 3

где - угловая скорость кривошипа по заданию,  и является ;

- длина кривошипа.

Направлен вектор  перпендикулярно кривошипу АВ в сторону направления угловой скорости .

Построение планов скоростей это графическое решение векторного уравнения. Для определения скорости точки С составляем два векторных уравнения:

                                                            (4)

                                            (5)

где  - вектор скорости точки С₀, принадлежащей неподвижной направляющей ползуна;

 - вектор относительной скорости точки С относительно точки С₀;

 - вектор относительной скорости точки С относительно точки В.

Вектор , как скорость неподвижной точки. Вектор  направлен параллельно x-x, т.к. точка С совершает поступательное прямолинейное движение относительно направляющей. Отсюда  и направлен параллельно x-x.

Вектор  перпендикулярен звену СВ, т.к. точка С совершает вращательное движение относительно точки В, при повороте кривошипа АВ.

В результате в векторном уравнении

Из шести показателей неизвестны только два, модули векторов  и , следовательно, векторное уравнение можно решить графически построением плана скоростей.

На чертеже выбираем произвольно полюс плана скоростей – точку Р. Из полюса откладываем произвольной длины отрезок , изображающий скорость точки В в направлении, перпендикулярном звену АВ в данном положении, в сторону направления угловой скорости . Примем отрезок .

Тогда масштаб планов скоростей будет:

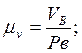                                                                                   (6)

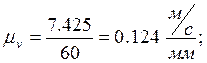
Отрезок  изображает вектор . Решая векторное уравнение через точку  проводим линию вектора  в направлении, перпендикулярном ВС, а через полюс Р линию вектора , совпадающего с вектором , параллельно направляющей x-x. Точка пересечения этих прямых определяет конец вектора РС, который изображает в масштабе  скорость точки С. Её величина определяется по формуле

                                                              (7)

где РС - вектор плана скоростей измеренный на чертеже, в мм.

Все вычисления занесены в таблицу 1.

Отрезок bc изображает относительную скорость , причём, стрелка вектора bc должна быть направлена в точку С, обозначая направление относительной скорости. Модуль скорости определяется с помощью масштаба .

                                                              (8)

где bc – вектор плана скоростей, измеренный на чертеже, в мм.

Определение  величины и направление углов скорости  шатуна

                                                                        (9)

Результаты вычислений сводим в таблицу 1.

Таблица 1

Параметры скоростей способом планов скоростей

положение параметры	0	1	2	3	4	5	6	6/	7	8	9	10	11
Рс, мм	0	39	62	62.5	44	20	4	0	25	45	58.5	57	37
	0	4,8	7.7	7.73	5,5	2.5	0,5	0	3.1	5,6	7,24	7.05	4.5
bс , мм	60	57	38	7	27	50	61	60	5.55	36.5	6.5	35	47,5
	7.4	7.05	4.7	0,9	3.3	6,2	7.5	7.4	6.9	4.5	0,8	4.3	5.9
	7.05	6.7	4.5	0,86	3.1	5.9	7.14	7.05	6.6	4.3	0,78	4.1	5.6

Примечание. Скорость  не включена в табл. 1, поскольку является постоянной.

Из анализа результатов расчётов видно, что движение точек и звеньев механизма характеризуется периодичностью.

1.2.3. Построение графика изменения силы полезного сопротивления