Структурный, кинематический и динамический анализ кривошипно-ползунного механизма и шарнирного четырёхзвенника, страница 8

Анализ данных таблицы 6 показывает, что наибольшую мощность сил полезного сопротивления  ползун развивает в девятом положении, т.е. наибольшую нагрузку механизм воспринимает именно в этом положении.

Дальнейший динамический анализ механизма проводим для девятого положения.

1.3.2. Определение инерционных нагрузок

Сила инерции звена механизма определяется по формуле

                                                                       (27)

где m – масса звена, кг;

, м/с² – ускорение центра масс звена механизма.

Прикладывается сила инерции в центре масс звена и направлена в противоположную сторону ускорения центра масс.

По условию задания масса звена

где l – длина звена и , принимая, что сечение звеньев механизма равномерное по всей длине, а удельное распределение массы по длине , масса кривошипа . Ускорение центра масс кривошипа в положении по таблице 3 . Получаем

Для шатуна: масса шатуна ; ускорение центра масс , сила инерции

Для ползуна: масса ползуна  (согласно заданию), , ускорение центра масс , сила инерции

Знак минус в формуле (27) для определения силы инерции звена показывает, что сила инерции направлена противоположно линейному ускорению центра масс звена.

Момент силы инерции звена механизма определяется по формуле:

                                              (28)

где  - момент инерции звена относительно оси, проходящей через центр масс перпендикулярно звену;

 - угловое ускорение звена.

По условию задания кривошип вращается с постоянной угловой скоростью, т.е. , поэтому его момент сил инерции .

Ползун перемещаясь поступательно по прямой направляющей так же имеет  и его момент .

Момент силы инерции шатуна определяется по формуле

где  - момент инерции шатуна. По условию задания шатун – относительно тонкий стержень и, тогда

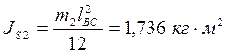
 по таблице 3 для девятого положения .

Тогда

Нм

1.3.3. Определение реакций в кинематических парах

Для определения реакций в кинематических парах воспользуемся принципами Даламбера и статической определимости групп Ассура. Вычерчиваем группу Ассура (звенья 2-3 ) в произвольном масштабе (можно использовать уже вычисленный масштабный коэффициент

= 0,0085м/мм), в положении 9. В соответствующих точках прикладываем силы действующие на группу Ассура: силы веса звеньев G₂ и G₃ в центрах масс, силы инерции ,  в центрах масс звеньев по линии действия линейного ускорения центра масс в противоположном направлении, силу полезного сопротивления F_C в точке С. Для удобства расчётов момент сил инерции  приводим к паре сил F_B = F_C^/, приложенных в точках В и С шатуна и направленных перпендикулярно линии ВС так, чтобы направление момента пары сил совпадало с направлением момента , а момент  направлен противоположно угловому ускорению .

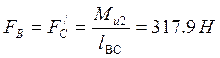                   (29)

Силы веса звеньев определяются по формуле:

                                                                (30)

где m – масса ,кг;

 - ускорение свободного падения .

;

;

;

Величина силы сопротивления в рассматриваемом 9-ом положении максимальна, т.е. .

Согласно заданию, центр масс ползуна  совпадает с точкой С, поэтому можно полагать, что реакцию  ползуна и направляющей проходит через точку С перпендикулярно направляющей x-x. Принимаем направление  вправо.

Из условия равновесия группы Ассура составляем уравнение суммы моментов сил, действующих на группу Ассура, относительно В.

Откуда определяем реакцию

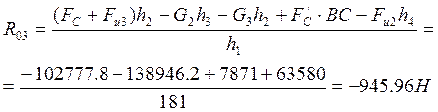
R₀₃ = -945.96 H

Величины отрезков ., ВС определяются замером на схеме.

Для определение реакции  в опоре В, направление которой заранее не известно так как опора шарнирная, составляем уравнение векторной суммы сил, действующих на группу Ассура в целом. Так как группа находится в равновесии, геометрическая сумма всех сил, действующих на её звенья, равно нулю.