Структурный, кинематический и динамический анализ кривошипно-ползунного механизма и шарнирного четырёхзвенника, страница 4

Силовой анализ механизма  выполняется для положения механизма, когда ползун развивает максимальную мощность . Для  определения  этого положения необходимо знать значение силы  во всех положениях механизма, для того, чтобы из произведений  выбрать наибольшее. Поэтому следует построить график, где S - путь ползуна.

Для этого параллельно движению ползуна проводим горизонтальную прямую – ось абсцисс, проведя к ней перпендикуляр из точки , получим точку 0 - начало координат, а проведя перпендикуляр из точки , получим точку –ограничивающую ход ползуна Н. Из точки 0 проводим ординат. По оси абсцисс откладываем отрезки аН и bН, восстанавливаем из полученных точек ординату до пересечении с прямой  произвольной длины (=60мм). Эта ордината выражает в масштабе  максимальную силу полезного сопротивления . Величину масштаба  найдем из выражения

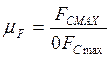                                                                           (10)

Соединив прямой линией все полученные выше точки, получим искомый график . При движении ползуна вверх сила  равна нулю , а при движении вниз сила  увеличивается по линейному закону до максимального значения. Проведя из точек вертикальные линии до пересечения их с графиком F_C(S), получаем соответствующие ординаты, , по которым определяем силы сопротивления , т.е. в любом положении механизма.

                                                                             (11)

где  - размер, измеренный на графике сил сопротивления для данного положения, в мм.

Результаты  вычислений сводим в таблицу 2

1.2.4. Определение ускорений точек звеньев механизма с помощью планов ускорений

Определяем ускорение точки В, совершающей равномерное вращательное движение. Оно определяется уравнением

                                                            (12)

где -ускорение неподвижной точки A ();

 - ускорение точки В во вращательном движении звена АВ вокруг точки А.

В свою очередь ускорение точки во вращательном движении складывается из тангенциального или касательного ускорения и нормального или центростремительного ускорения

                                                         (13)

где  - тангенциальное  ускорение точки В во вращательном движении, в м/с²;

 - нормальное ускорение, в м/с².

                                                            (14)

где  - угловое ускорение точки В во вращательном движении вокруг точки А.

Так как точка В совершает равномерное вращательное движение вокруг точки А (по условию задания), то , значит .

Определяем нормальное ускорение

                                                          (15)

Отсюда  и направлено ускорение по радиусу к центру вращения, т.е. от В к А.

Таким образом, полное ускорение точки В будет

Для определения ускорения точки С составим два векторных уравнения;

                                                        (16)

и ускорение точки С, принадлежащей шатуну ВС, в плоскопараллельном движении ползуна

                                                               (17)

Рассмотрим первое уравнение (16):

 - ускорение точки С₀, неподвижной направляющей (звено 0), равно нулю, ;

 - нормальное ускорение точки С в движении относительно точки С₀, т.е. направляющей, тоже равно нулю, т.к. движение поступательное, ;

 - тангенциальное или касательное ускорение точки С в движении относительно точки С₀, направлено по касательной к траектории движения, т.е. вдоль направляющей x-x, модуль её пока не известен. И так  и направлен вдоль x-x.

Второе уравнение (17)

 - известно и по модулю и по направлению, ;

 - нормальное (центростремительное) ускорение точки С во вращательном движении звена ВС относительно точки В, по величине равно:

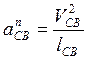                                                                   (18)

Направлено  вдоль линии ВС от точки С к точке В. Все расчеты сведены в таблицу 3.