Структурный, кинематический и динамический анализ кривошипно-ползунного механизма и шарнирного четырёхзвенника, страница 5

 - тангенциальное (касательное) ускорение точки С во вращательном движении звена ВС относительно точки В, направлено по касательной к траектории движения, т.е. перпендикулярно линии ВС, по величине не известно.

Во втором векторном уравнении только два неизвестных, это модули векторов  и , направление которых известно, значит оно решаемо графически.

Решаем графически второе векторное уравнение построением планов ускорений.

Выбираем произвольную точку П (полюс плана ускорений) и из него параллельно линии ВА в направлении от В к А проводим отрезок Пв произвольной длины (в нашем случае Пв=140мм), выражающий в масштабе  ускорения . Величина масштаба плана ускорений определяются по формуле:

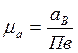                                                                     (19)

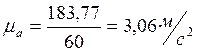
К вектору  прибавляем вектор , т.е. из точки в проводим параллельно линии СВ в направлении от СВ прямую линию и на ней откладываем отрезок , изображающий направления ускорения , равный

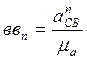
Значения  для 12 положений показаны в таблице 3.

Через конец вектора (точку ) проводим прямую линию перпендикулярную , изображающую направление вектора , т.к. вектор  направлен вдоль СВ, а вектор  направлен перпендикулярно СВ.

Так как, сjгласно первому векторному уравнению, вектор  направлен вдоль направляющей x-x, из полюса П проводим прямую линию параллельно траектории движения ползуна – направляющей x-x. На пересечении векторов  и  находится точка С – конец вектора ПС, изображающего ускорение  в масштабе  и конец вектора , изображающего ускорение .

Определим модули этих ускорений и заносим их значения в таблицу 3.

Угловое ускорение звена ВС определяется по формуле

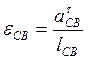                                                                   (20)

Для определения направления углового ускорения  мысленно закрепим точку B, а вектор с плана ускорений перенесём в точку C механизма. Под действием этого вектора звено ВС будет стремиться, повернутся вокруг точки В. Это, и будет направлением .

Для определения ускорений центров масс звеньев считаем, что центры масс располагаются в геометрическом центре звеньев, центр масс ползуна S совпадает с центром масс шарнира С. намечаем на плане ускорений точки S₁ – середина отрезка Пв (центр масс кривошипа) и S₂ – середина отрезка вС – центр масс шатуна (на основании теоремы подобия или свойства пропорциональности между планом ускорений и планом механизма). Точку S₂ соединим с полюсом П.

Тогда,

Таким образом определяются линейные ускорения точек В, С, S₁, S₂ и угловые ускорения шатуна ВС для всех 12-ти положений механизма и их параметры заносим в таблицу3

Таблица 3

Параметры планов ускорений