Общая характеристика пакета программ «Надежность», страница 6

Рекуррентная модель учитывает неоднородность исходных статистических данных, текущей и априорной информации об отрабатываемой конструкции (неоднородность, обусловленную воздействиями на испытываемое изделие в процессе его отработки в виде доработок, варьированием «конфигурацией» объекта испытаний, разнообразием режимов и условий испытаний) основывается на использовании идеи формулы полной вероятности. При этом, вероятность осуществления события А, состоящего в безотказном функционировании изделия после проведения доработки (изменения режима испытаний):

, где  - вероятность осуществления гипотезы, заключающейся в том, что доработка (изменение режима испытаний) не изменила надёжности изделия и результаты испытаний до и после доработки принадлежат одной генеральной совокупности. Оценки  вероятности  и  вероятности  определяются:

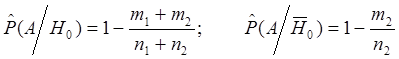, где m₁ и m₂ - число отказов в испытаниях до и после доработки, соответственно; n₁ и n₂ - число испытаний до и после доработки, соответственно.

Тогда оценка  вероятности Р(А) определяется:

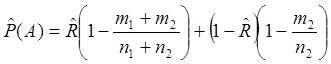, где  - оценка вероятности осуществления гипотезы Н₀;  - оценка вероятности осуществления гипотезы альтернативной Н₀;  - весовой коэффициент, имеющий смысл вероятности осуществления гипотезы Н₀ об однородности статистических данных. При : ; при : ; в реальных условиях отработки .

Используются различные подходы к расчёту оценки  весового коэффициента. В работе [6] предложена следующая модель такого расчёта:

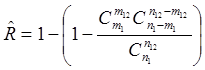, где m₁ и n₁ - число отказов и число испытаний до доработки; m₂ и n₂ - число отказов и число испытаний в серии после оцениваемой доработки до следующей доработки; m₁₂ = m₁ + m₂ и n₁₂ = n₁ + n₂.

При представления исходных данных в виде величин , , , представляющих собой количество испытаний и отказов после () доработки и до -ой доработки (, — исходы испытаний до первой доработки, , — исходы испытаний после последней m-ой доработки) определяется оценка вероятности не наступления отказов  для данного этапа отработки (после  доработок) в соответствии с многошаговой процедурой, изложенной ниже.

На первом шаге учитывается эффективность только первой доработки.

При этом используются данные:

 — количество испытаний и число отказов i-го типа до проведения первой доработки;

 — количество испытаний и число отказов i-го типа в период от первой до второй доработки.

По этим данным определяется весовой показатель  (вероятность того, что первая доработка () не изменила надежности блока):

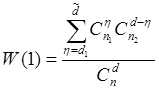,   где , , .

Оценка вероятности не наступления отказа данного типа после проведения первой доработки     .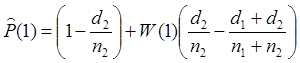

Эквивалентный объем испытаний (до второй доработки или общий, если последней доработки не было)  ,  эквивалентное число отказов .

На второй шаге вычислений учитывается эффект второй доработки. При этом в качестве исходных данных аналогично принимаются величины:  — эквивалентные исходы испытаний до второй доработки;  — количество испытаний и число отказов i-го типа от второй до третьей доработки.

По этим данным определяется весовой показатель  (вероятность того, что вторая доработка не изменила надежности блока).

Оценка вероятности не наступления отказа данного типа после проведения второй доработки по результатам испытаний до третьей доработки

.

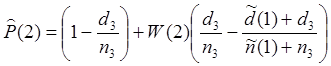Эквивалентный объем испытаний (до третьей доработки или общий) , эквивалентное число отказов .

Аналогично вычисляются оценки  с учетом эффективности всех последующих доработок, .

Конечная оценка вероятности не наступления отказов  (после проведения всех доработок)  .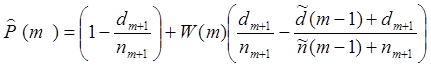

Эквивалентный объем испытаний , эквивалентное число отказов .

Нижняя доверительная граница  уровня  или (1-γ,-,+1).

          Модель дифференцированная по причинам отказов [5].

Точечная оценка вероятности безотказной работы при наличии отказов определяется по формуле 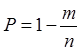, где n - число выстрелов за период испытаний; m – число отказов при n выстрелах.

Точечная оценка вероятности безотказной работы при отсутствии отказов определяется по формуле 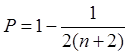, где n - число выстрелов за период испытаний.