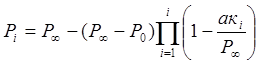Общая характеристика пакета программ «Надежность», страница 5

, где .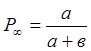                        

Для решения задачи статистического оценивания параметров модели а, Р₀ и  по результатам отработки изделия может быть использован метод максимального правдоподобия, применение которого предполагает справедливость допущения о независимости результатов испытаний. Исследование статистической независимости результатов испытаний, относящихся к разным этапам (после i-ой и ()-ой доработок) сводится к определению и исследованию корреляционного момента дискретной случайной величины X (отражающей исход j-го испытания после i-ой доработки) и Y ((j+к)-го испытания после ()-ой доработки):  , где m_x, m_y - математические ожидания случайных величин X и Y.

После преобразования: , где      P_i = P_j - вероятность успеха в j-м испытании;   - условные вероятности успеха в (j+к)-м испытании после (i+z)-й доработки, если в j-м испытании был отказ х_1j или успех х_2j. Коэффициент корреляции величин X и Y равен:

 .

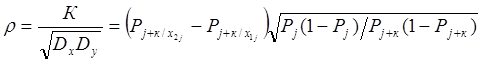В соответствии с принятыми допущениями изменение вероятности от P_j до Р_j+к происходит только из-за внесения доработок, которые возможны после успешных испытаний или отказов. Факты внесения доработок не связаны с исходами испытаний и являются достоверными событиями. Это предопределяет статистическую независимость исходов испытаний, т.е. вероятности   и   являются  безусловными  и  равными  между собой и . В силу показанной независимости результатов испытаний вероятность получения  отказов в n_i испытаниях определяется биномиальным выражением 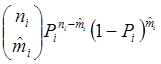. Вероятность получения всей выборки (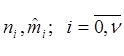), т.е. функция правдоподобия, определяется произведением вероятностей: 

.

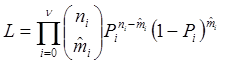При этом,                              

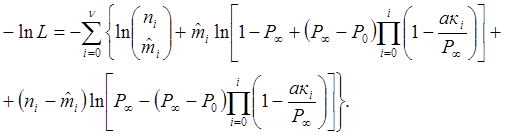
В качестве оценок максимального правдоподобия принимаются значения   ,  при которых  функция  правдоподобия  при  заданной выборке () обращается в максимум (- lnL в минимум). Получаемые оценки максимального правдоподобия являются состоятельными, асимптотически несмещенными и асимптотически эффективными (для больших выборок). Предельным законом распределения оценок максимального правдоподобия является  трёхмерный  нормальный  закон распределения со средним значением

() и матрицей ковариаций:

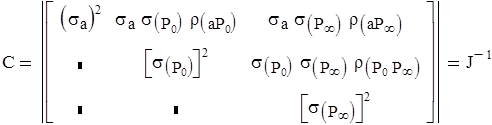
Здесь J - информационная матрица Фишера, элемент которой равен:

.

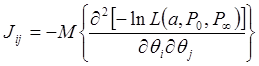Точность оценок параметров  можно определить, если в выражении для С или J вмеcто истинных значений параметров а, Р₀,  подставить оценки максимального правдоподобия . Дисперсия  оценки Р_i может быть найдена путём замены нелинейной зависимости для Р_i, линеаризованной:

.

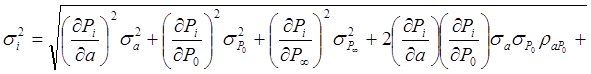
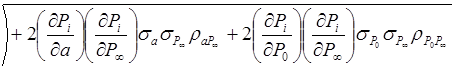При нормальном законе распределения оценки  доверительный интервал для оценки  в каждом сечении процесса (считая  со средним квадратическим отклонением ):

- двухсторонний доверительный интервал с коэффициентом доверия  ;

- односторонний нижний доверительный предел , где  - квантиль нормального распределения.

В практических задачах при анализе точности исследования надёжности отрабатываемых изделий рекомендуется, в целях упрощения расчётов, оценивать сверху среднее квадратическое отклонение оценки ПН на последнем этапе (после последней доработки) по формуле:    .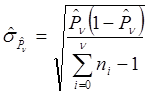

Рассмотренная модель роста надёжности отрабатываемого изделия при дополнительных упрощающих допущениях (в каждой доработке устраняется одинаковое количество причин отказов к_i=к=const и при проведении n испытании  доработок проводятся равномерно, т.е. существует линейная зависимость между номером доработки i и номером испытании j   ) сводится к модели математического ожидания: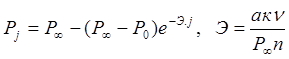 ,  описывающей изменение надёжности отрабатываемого изделия в зависимости от номера испытаний j.

Основная сфера применения упрощенных моделей роста надёжности - задачи прогнозирования. При этом, считая частоту доработок  аналогом вероятности проведения доработки, становится возможным определение величины этой характеристики при прогнозировании процесса изменения надёжности отрабатываемой конструкции по данным отработки подобных образцов в близких условиях.

Рекуррентная модель (дифференцированная по доработкам) [4].