В теории надёжности отсутствует единственный универсальный и одновременно эффективный метод оценки ПН отрабатываемого изделия. Не закрыт вопрос и об определении областей эффективного применения различных методов и моделей. Из этого следует, что ни одной из моделей в отдельности недостаточно для точной и достоверной оценки ПН отрабатываемого АО. Очевидной перспективой в поиске эффективных методов оценки ПН отрабатываемого АО оказывается применение комплексного алгоритма оценки ПН, объединяющего сильные стороны известных методов: метода, использующего аппроксимирующую модель (модель роста надёжности - модель реализации процесса изменения надёжности объекта при отработке); методов, основывающихся на построении рекуррентных соотношений с использованием формулы полной вероятности; классический метод обработки результатов испытаний, проводимых по схеме Бернулли (биномиальных испытаний).
3.2. Сравнительный анализ моделей оценки надежности АС в процессе отработки и испытаний.
Модели оценки надежности АС в процессе отработки и испытаний.
Биномиальная модель [2].
В модели, относящейся к схеме испытаний Я. Бернулли,
рассматривается последовательность n независимых испытаний, в каждом из которых
возможны два исхода: А и ![]() (например, успех и отказ). Вероятности
исходов равны р и q
соответственно, причем р = 1 –
q. В каждом испытании вероятность р постоянна. При этих предпосылках
рассматривается случайная величина t — возможное число исходов вида
(например, успех и отказ). Вероятности
исходов равны р и q
соответственно, причем р = 1 –
q. В каждом испытании вероятность р постоянна. При этих предпосылках
рассматривается случайная величина t — возможное число исходов вида ![]() (например,
отказов) в n
испытаниях. Вероятность
(например,
отказов) в n
испытаниях. Вероятность ![]() того, что в n
испытаниях будет ровно
того, что в n
испытаниях будет ровно ![]() отказов,
и вероятность
отказов,
и вероятность ![]() того, что в n
испытаниях число отказов не превысит некоторого фиксируемого значения х, выражаются с помощью
соотношений
того, что в n
испытаниях число отказов не превысит некоторого фиксируемого значения х, выражаются с помощью
соотношений 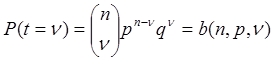 ,
,
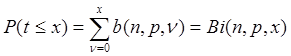 , где
, где
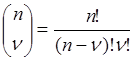 .
. ![]() и
и ![]() - обозначения, используемые далее для
сокращения записи.
- обозначения, используемые далее для
сокращения записи.
Здесь n и р параметры,
а выражение ![]() — функция биномиального
распределения. Корни
— функция биномиального
распределения. Корни![]() и
и![]() уравнений
(Клоппера-Пирсона)
уравнений
(Клоппера-Пирсона) ![]() ,
, ![]() ,
, ![]() являются
соответственно верхней и нижней границами доверительного интервала [
являются
соответственно верхней и нижней границами доверительного интервала [![]() ] для параметра p, причем
] для параметра p, причем ![]() .
.
В
приведенных уравнениях величина d — число наблюденных (зарегистрированных)
исходов ![]() (отказов) в n испытаниях;
(отказов) в n испытаниях; ![]() — доверительная вероятность.
— доверительная вероятность.
Корни ![]() и
и ![]() выражаются в виде соотношений
выражаются в виде соотношений ![]() ,
, ![]() , вычисляемые через неполную
бэта-функцию (
, вычисляемые через неполную
бэта-функцию (![]() ).
).
Аппроксимационная модель [3].
Аппроксимирующая модель характеризуется допущениями: испытания в процессе отработки изделия делятся на этапы моментами внесения доработок; внутри этапа испытания (опыты) независимые; надёжность объекта испытаний изменяется только в результате доработок; доработка может проводиться как после отказа, так и после успешного испытания; относительный вклад каждой доработки в изменение надёжности изделия выражается числом устранённых причин отказов; вклад устранения одной причины отказа в изменение надёжности отрабатываемого изделия постоянный для данного периода испытаний.
Модель
строится на основе логико-вероятностного принципа. При этом, анализируются в
виде линейной аппроксимации приращения значений оцениваемого ПН (![]() - приращение вероятности безотказной
работы) в результате проведения доработок конструкции.
- приращение вероятности безотказной
работы) в результате проведения доработок конструкции.
![]() , где аi
- коэффициент, характеризующий изменение оставшейся после (i-1)-ой
доработки вероятности отказа (1–Рi-1) за счёт i-ой
доработки; вi - коэффициент, характеризующий снижение
достигнутой вероятности безотказной работы Рi-1 за счёт i-ой
доработки; i - индекс, характеризующий номер доработки (
, где аi
- коэффициент, характеризующий изменение оставшейся после (i-1)-ой
доработки вероятности отказа (1–Рi-1) за счёт i-ой
доработки; вi - коэффициент, характеризующий снижение
достигнутой вероятности безотказной работы Рi-1 за счёт i-ой
доработки; i - индекс, характеризующий номер доработки (![]() - количество доработок). Известна связь i
= i(j), где j - номер опыта в последовательности испытаний (
- количество доработок). Известна связь i
= i(j), где j - номер опыта в последовательности испытаний (![]() - объём испытаний). Линейная модель
учитывает возможность как повышения, так и снижения достигнутого значения Рi-1,
т.е.
- объём испытаний). Линейная модель
учитывает возможность как повышения, так и снижения достигнутого значения Рi-1,
т.е. ![]() . Коэффициент ai
характеризует эффективность проведенной доработки изделия, т.е. долю
вероятности отказа, преобразуемую в приращение
. Коэффициент ai
характеризует эффективность проведенной доработки изделия, т.е. долю
вероятности отказа, преобразуемую в приращение ![]() .
Коэффициент вi характеризует негативную сторону доработки и
количественно определяет степень уменьшения достигнутой Рi-1.
Значение коэффициента аi определяется объёмом получаемой при
испытаниях информации, позволяющей достоверно устанавливать и устранять причины
отказов, значение коэффициента вi - информации, анализ
которой привел к ошибочным выводам относительно причин отказов и,
соответственно, к доработкам, снижающим ПН. Естественно, что чем больше причин
отказов устраняется одной доработкой, тем существеннее её влияние на ПН
изделия. Поэтому вводится предположение, что аi = кia;
вi = кiв, где кi - количество
устраняемых i-ой доработкой причин отказов; а, в - постоянные
коэффициенты, характеризующие эффективность устранения одной причины отказа.
Таким образом, функция изменения ПН отрабатываемого изделия имеет вид:
.
Коэффициент вi характеризует негативную сторону доработки и
количественно определяет степень уменьшения достигнутой Рi-1.
Значение коэффициента аi определяется объёмом получаемой при
испытаниях информации, позволяющей достоверно устанавливать и устранять причины
отказов, значение коэффициента вi - информации, анализ
которой привел к ошибочным выводам относительно причин отказов и,
соответственно, к доработкам, снижающим ПН. Естественно, что чем больше причин
отказов устраняется одной доработкой, тем существеннее её влияние на ПН
изделия. Поэтому вводится предположение, что аi = кia;
вi = кiв, где кi - количество
устраняемых i-ой доработкой причин отказов; а, в - постоянные
коэффициенты, характеризующие эффективность устранения одной причины отказа.
Таким образом, функция изменения ПН отрабатываемого изделия имеет вид: 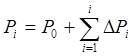 , где Р0 - значение ПН
изделия до первой доработки. После преобразований, проведенных по рассмотренной
схеме, выражение для модели роста ПН отрабатываемого изделия приобретает вид:
, где Р0 - значение ПН
изделия до первой доработки. После преобразований, проведенных по рассмотренной
схеме, выражение для модели роста ПН отрабатываемого изделия приобретает вид:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.