Оценка надежности систем на этапе экспериментальной отработки, страница 6

, координаты которого независимы. Будем считать, что состояние работоспособности на момент  может быть задано условием:

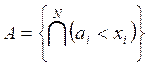 или 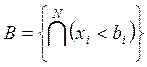, т.е. на каждый определяющий параметр  задан односторонний (нижний или верхний) допуск. Случай двухсторонних ограничений можно свести к рассматриваемому. Тогда показатель надежности Р, представляющий собой вероятность функционирования изделия на момент , примет вид:

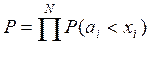 или .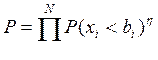

Если дополнительно принять закон распределения i-го параметра  нормальным с неизвестными параметрами  и , то показатель Р можно представить в ви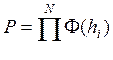де:

, где  или ,  - функция Лапласа.

В частности,  может играть роль наработки до отказа, и тогда  - это заданное время функционирования i-ой компоненты изделия.

При испытаниях изделия измеряются величины  - выборочные значения вектора определяющих параметров , по которым можно найти для каждого  выборочные оценки параметров ,  и :

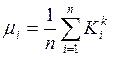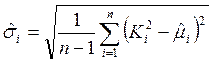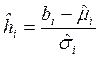, ,  или 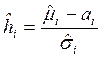, на основании чего можно определить точечную оценку и НДГ Р уровни  для показателя Р [18].

Наша задача состоит в определении вероятности гипотезы  при различных альтернативах, где  и  - нормированные допуски на i-ый определяющий параметр  в условиях испытаний  и  соответственно.

Поскольку, по предположению, параметры  независимы, достаточно рассмотреть правило определения вероятности гипотезы  по результатам  измерений параметра . Для краткости индекс 1 будем ниже опускать.

При сделанных предположениях о законе распределения  статистика  имеет нецентральное распределение Стъюдента с () степенью свободы и параметром нецентралъности , которое приближенно можно аппроксимировать нормальным распределением со средним  и дисперсией 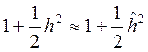, т.е. принять, что      

.

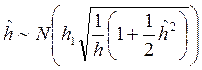Тогда статистика

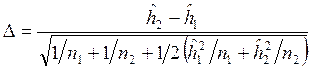                                    ,                                (З.14)

будет иметь стандартньй нормальный закон, если гипотеза  верна.

Следовательно, -значение гипотезы  при альтернативе  может быть определено обычным образом на основе формулы (3.2а) в виде:

                                                    ,                                              (3.15)

где  определяется по формуле (З.14), исходя из оценок  и , полученных по результатам испытаний на первом и втором этапах соответственно (предполагается, что ).

Формулу (3.15) можно использовать для определения вероятности  любой гипотезы .

Пример 2. Пусть на первом этапе испытаний было проведено  = 10 измерений параметра X и получено значение  = 2,33, а на втором этапе (в условиях ) проведено  = 4 измерения и найдено значение  = 1,65.

Поскольку , естественно исходить из гипотезы . По формуле (3.14) находим  = - 0,71, после чего на основании общего правила (3.2а) и с учетом выражения (3.15) имеем:

.

4. Методика оценки надежности изделий при наличии доработок

Приведенные в разделе 2 расчетные формулы (и ни аналогичные) позволяют найти объединенные оценки  и  показателя надежности изделия (Р) по результатам испытаний в двух различных режимах. В частности, их можно использовать при расчете надежности изделия, на котором была проведена одна доработка конструкции. Если же в ходе экспериментальной отработки изделия доработки проводились неоднократно, то указанные формулы нужно использовать последовательно несколько раз. Методика оценки надежности изделий в этих условиях применительно к различным планам испытаний изложена ниже.

4.1. Форма представления данных

Будем предполагать, что изделие состоит из  последовательно соединенных независимых блоков (сборочных единиц), так что

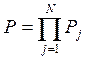, где  - показатель надежности j-го блока (), представляющий собой вероятность безотказного функционирования изделия за требуемое время.

Отработка изделия и его блоков ведется на этапах автономных и комплексных испытаний, причем на каждом этапе определяются оценки показателей надежности блоков  и изделия в целом Р в виде точечных оценок ,  и в виде НДГ ,  заданного уровня .

Поскольку методы расчета оценок надежности изделия в целом на основе соответствующих оценок для его частей (блоков) достаточно хорошо изучены [21, 22], будем рассматривать здесь лишь правила расчета оценок  и , причем для кратности индекс  опустим.