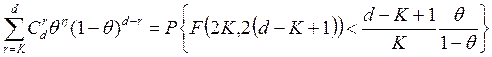Оценка надежности систем на этапе экспериментальной отработки, страница 5

, где  - случайная величина, имеющая F-распределение Фишера с  и  степенями свободы.

Полагая , , , получаем для  следующее представление (если ):

    (3.9).

Если , то индексы 1 и 2 в представлении (3.9) меняются местами. Наиболее полные таблицы квантилей F-распределения приведены в работе [19].

Нормальная аппроксимация биноминального закона справедлива при  и приводит к следующей формуле [16]:

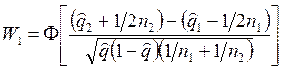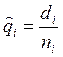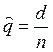, ,       (3.10).

Формула (3.10) получена для гипотезы , в cлyчaе гипотезы  индексы 1 и 2 в (3.I0) нужно поменять местами.

Сравнение формул (3.6) и (3.9), (3.10), приведенное в таблице 3.1, показывает, что приближения (3.9) и (3.10) хорошо работают даже при малых объемах выборок.

Таблица 3.1

	1/0			1/1
	5/5	5/10	5/20	5/5	5/10	5/20
Точная формула Нормальная аппроксимация Пуассоновская аппроксимация	0,5 0,5 0,5	0,33 0,36 0,51	0,2 0,22 0,19	0,78 0,785 0,75	0,57 0,6 0,54	0,37 0,42 0,34

б. Планы испытаний с измерением наработки до отказа

Рассмотрим распространенный на практике случай, когда наработка до отказа  подчиняется экспоненциальному закону надежности.

В соответствии с работами [1, 17] различают планы испытаний типа , с фиксированной продолжительностью Т, и типа  - с допустимым числом отказов . Рассмотрим оба случая.

Пусть испытания проводятся по плану  и пусть на первом этапе из  образцов за время Т₁ отказало , a  - знамения наработок отказавших образцов. Аналогичная информация имеется по результатам второго этапа испытаний: , , .

Считая, что изделия обладает высокой надежностью, можно принять поток их отказов пуассоновским - с параметрами  и  на первом и втором этапax ( - вероятности отказа образца на i-oм этапе за время испытаний,  - параметр потока отказов на i-ом этапе).

Тогда проверка гипотезы  (или ) эквивалентна проверке гипотезы  том, что неизвестные средние  и  двух независимых случайных величин , и  с пуассоновским законом распределения находятся в заданном отношении. Нетрудно показать [16], что условное распределение случайной величины  при условии  и сделанных предположениях имеет вид

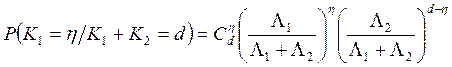, откуда с учетом связи между биноминальным распределением и F-распределением Фишера имеем

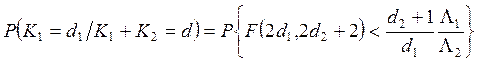                    .                      (3.11)

С учетом общей формулы (3.1a) имеем для W-значения гипотезы Н₀ при альтернативе  следующее выражение

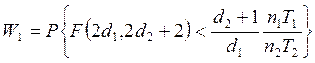                               .                                     (З.12)

Пусть теперь испытания проводятся по плану , причем результаты испытаний на первом и втором этапах соответственно равны:  и , где  и  - наработки до отказов.

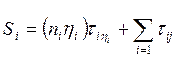Пусть найдены суммарные наработки ,  при плане R и  при плане U.

Тогда случайная величина  имеет -распределение с  степенями свободы , а следовательно, статистика

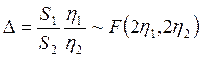
имеет F-распределение Филера с  и  степенями свободы, если только гипотеза  верна.

Поскольку альтернатива  тем лучше согласуется с опытными данными, чем меньше наблюденное значение статистики , для определения  - значения нужно воспользоваться формулой (3.2а), на остове которой получаем:

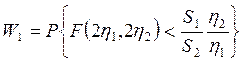                                        .                                       (3.13)

При альтернативе , нужно в формуле (3.13) индексы 1 и 2 поменять местами.

В заключение этого пункта отметим, насколько полученные результаты можно обобщить.

Предположение об экспоненциальности закона распределения наработки до отказа Т можно заменить (с несложным изменением формул) на предположение о том, что распределение является вейбулловским - с известным параметром формы.

Для нормального закона распределения  расчетные формулы приводятся ниже. Если закон распределения наработки до отказа неизвестен вовсе, следует использовать биноминальный план испытаний.

в. План испытаний с измерением определяющих параметров

Предположим, что состояние изделия на заданный момент времени можно задать N-мерным случайным вектором: