Оценка надежности систем на этапе экспериментальной отработки, страница 4

Более удобной процедурой проверки гипотезы , в определенном смысле обратной к изложенной выше, является следующая. Вместо того, чтобы работать с фиксированным уровнем значимости  и только соглашаться с принятием или отклонением , мы могли бы найти по формулам (3.1) - (3.2) такое значение  (будем обозначать его W), которое соответствует реализации Т₀ статистики Т, наблюденной в данном эксперименте (в данной выборке). Эту величину  называют по-разному: «фактически достижимым уровнем значимости» в работе [15], «W–значением» а работе [16] и т.п. Фактически величина есть вероятность тoгo, что статистика Т, по которой ведется проверка гипотезы , примет следующие значения (при условии, что  верна):

а) большее, чем ее наблюденное значение Т₀, при , и тогда

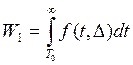     (3.1a), б) меньшее, чем ее наблюденное значение Т₀, при , и тогда

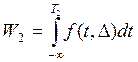     (3.2a), или, что все равно,      .

В случае двусторонней альтернативы  величина W определяется (если принять равными «хвосты» распределения  над критической областью) из условия

                                                                                                                         

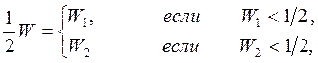
или, что все равно,       (3.3a).

Формулы (3.1а) - (3.3а) являются следствием формул (3.1) - (3.2) и позволяют определить «W-значение», или вероятность гипотезы Н₀, при произвольном законе распределения  статистики Т. Если статистика Т является дискретной случайной величиной, то интегралы в формулах (3.1а) - (3.3а) переходят в соответствующие суммы.

Перейдем к выводу конкретных рабочих формул для определения показателя W по выборочным данным при различных планах испытаний.

а. Биноминальный план испытаний

Пусть  и  - результаты испытаний изделия на i-ом этапе в условиях . Обозначим через  возможное число отказов из  образцов. Случайные величины  независимы и имеют биноминальный закон распределения с параметром , который определяет вероятность безотказной работы изделия в режиме .

Требуется по результатам испытаний оценить вероятность W гипотезы  при альтернативах Н₁, Н₂ или Н₃.

Пространство исходов опыта  состоит из точек , . Для определенности будем считать, что . В противном случае второй этап испытаний будем считать первым. Положим , .

Нетрудно показать, что условное распределение случайной величины     (или ) при том, что , является гипергеометрическим, если гипотеза Н₀ верна, т.е.

                         , ,                  (3.4)

где  - число сочетаний из n по d.

Действительно, вероятность появления исхода () с учетом независимости  равна

     (3.5).

Если верна гипотеза , то выражение (3.5) принимает вид

.

С другой стороны, если Н₀ верна, то

.

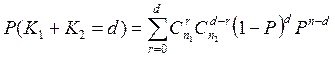По определению условной вероятности получаем

    .

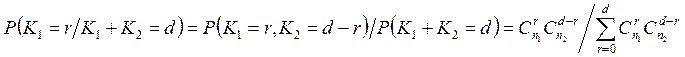Учитывая, что 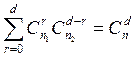, приходим к равенству (3.4).

Используя условное распределение (З.4) случайной величины , которое получено в предположении, что Н₀ верна, и соотношение (3.1а), приходим к выводу, что при альтернативе  (или , )  - значение определяется по формуле (если )

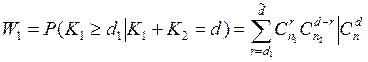,       (3.6).

Если , то, меняя местами индексы 1 и 2 (т.е. считая первый этап испытаний вторым, и наоборот), придем снова к формуле (3.6).

При альтернативе  (или ) W - значение определяется с учетом выражения (З.2а) по формуле

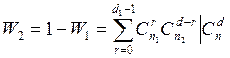   при ()     (3.7).

Наконец, при альтернативе  W - значение определяется в соответствии с формулой (З.За):

     (3.8).

Пример 1. Пусть  = 3,  = 1 и  = 8,  = 2, т.е. 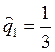, 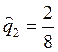. Найдем вероятность гипотезы  против каждой из альтернатив H₁, Н₂ и Н₃.

По формуле (3.6) (учитывая, что ) находим

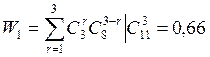.    По формулам (3.7) и (3.8):

 и .

Формулы (3.6) - (3.8) являются точными при любых значениях  и , однако при  > 10 и  > 2 вычисления по ним довольно громоздки. Поэтому при больших значениях  и  удобней использовать их приближения, основанные на замене биноминального закона распределения законом Пуассона или нормальным распределением.

Пуассоновское приближение биноминального закона справедливо при условии, что [1]    и , и при этом:

.

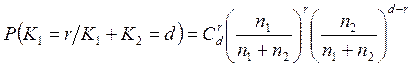Используя связь между функцией биноминального распределения и F- распределением Фишера [16], можно записать