Оценка надежности систем на этапе экспериментальной отработки, страница 2

Проверка гипотезы  осуществляется по выборочным данным двух этапов испытаний на основе одного из статистических критериев. В том случае, когда гипотеза  принимается, оценка показателя Р, производится на основе информации по всем испытаниям. Если же гипотеза  отвергается, то оценка показателя Р определяется по результатам того этапа испытаний, который в наибольшей степени согласуется с условиями будущей эксплуатации изделия. При этом достоверность (или точность) оценок, естественно, снижается.

При таком подходе проверка однородности статистических данных носит дискретный характер: предварительная информация полностью используется или полностью отбрасывается, хотя «степень соответствия» данных на различных этапах испытаний меняется непрерывно. Это приводит, с одной стороны, к неоправданным скачкам оценок  и , а с другой стороны - к набору малодостоверных оценок, которыми невозможно пользоваться для определения фактического уровня надежности после заключительного этапа испытаний.

Перейдем к рассмотрению другого способа объединения информации, который в отличие от изложенного назовем непрерывным.

Обозначим через  оценку вероятности безотказной работы изделия, найденную в предположении, что верна гипотеза , а через  - оценку вероятности безотказной работы, найденную в предположении, что верна одна из конкуриющих гипотез: или    (2.1), если есть основания считать, что на втором этапе надежность снизиться не может (например, проведена доработка, заведомо повышаюшая надежность изделия или    (2.2), если есть основания считать, что условия испытаний на втором этане являются более жесткими, или    (2.3), если ничего определенного относительно характера изменения надежности изделия на различных этапах испытаний сказать нельзя.

Будем также считать (для определенности), что условиям будущей эксплуатации изделия отвечает именно последний (второй) этап испытаний. Это значит, что в случае отклонения гипотезы  оценка  вероятности безотказной работы должна определяться по результатам испытаний последнего (второго) этапа.

С учетом предыдущих обозначений и предположений для оценок  и   справедливы следующие известные выражения

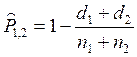    (2.4),  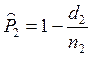      (2.5).

Как уже отмечалось, стандартный подход предписывает использовать оценку , если принята гипотеза , и оценку  - если принята альтернативная гипотеза (одна из ). Между тем вероятность принятия гипотезы  меняется непрерывно в интервале (0,1), и назначение некоторого порога для нее, начиная с которого нужно скачком менять оценку  на , представляется довольно искусственным приемом.

Гораздо естественнее выбор между двумя вариантами оценок производить путем их усреднения с весовыми коэффициентами, имеющими смысл вероятностей выбора каждой из двух ситуаций.

Иными словами, оценку  вероятности безотказной работы изделия по объединенной информации предполагается искать в виде

    (2.6), где W - весовой коэффициент, имеющий смысл вероятности выбора гипотезы об однородности статистических данных, т.е. в рассматриваемом случае, гипотезы .

Из выражения (2.6) следует, что при  (т.е. когда гипотеза  применяется) , а при W  0 (когда  заведомо отклоняется) . Это означает, что формула (2.6) дает, как частные случаи, те выводы, которые делаются при стандартном подходе. Однако она дает ответ и в любой другой ситуации, когда величина  далека от крайних значений 0 и 1, что позволяет говорить о непрерывном учете степени неоднородности выборочных данных. Правило оценки показателя W будет изложено ниже.

Для характеристики точности полученной оценки (и ее достоверности) нужно указать правило определения НДГ  уровня  для показателя . С этой целью преобразуем исходы испытаний на обоих этапах в некоторые эквивалентные исходы испытаний. Правило такого преобразования будет зависеть от плана испытаний на данных этапах. Приведем его для случая биноминального плана испытаний (для других планов испытаний его вывод аналогичен).