Оценка надежности систем на этапе экспериментальной отработки, страница 3

Пусть на каждом из двух этапов испытания изделия дали следующие исходы: ,  для первого этапа и ,  - для второго, где  - число образцов на i-ом этапе, поставленных на испытания,  - число отказавших образцов, . На основании этих данных можно найти оценки , ,  и следовательно, по формуле (2.6) определить объединенную оценку , на основании которой легко установить эквивалентные исходы испытаний  и .

Под эквивалентным количеством испытаний  и отказов , соответствующих рассматриваемым двум этапам испытаний, будем понимать такие исходы биноминальных испытаний  и , при которых оценка показателя Р равна уже найденной величине и  по формуле (2.6). Это условие можно записать в следующем виде (если использовать для биноминального параметра Р   оценку максимального правдоподобия);

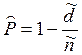,  откуда         .

Для определения  заметим, что испытания на втором этапе соответствуют требуемым условиям полностью, а условия проведения испытаний на первом этапе соответствуют требуемым лишь с вероятностью . Поэтому из всех  испытаний на первом этапе лишь их доля, равная , соответствует требуемым условиям. Следовательно:

   (2.7), где  [x] - означает целую часть числа x.

Величина  может принимать дробные значения, однако это не влияет на конечные выводы, которые могут быть сделаны на основании величин  и . Именно, определив  и  по формулам (2.6) и (2.7) соответственно, НДГ  уровня  находим по таблицам [3] в виде: 

   (2.8), где  - квантиль, неполная бета-функция, табулированная в работе [3].

При  вместо таблиц [3] можно использовать приближенную формулу 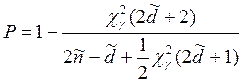    (2.9), где  - квантиль -распределения с к степенями свободы уровня  (при дробных значениях «к» надо пользоваться линейной интерполяцией табличных значений квантилей).

Итак, формулы (2.6), (2.8), (2.9) позволяют определять оценки  и  показателя надежности изделия  по результатам испытаний с учетом степени их «разнородности», которая учитывается весовым коэффициентом .

3. Определение весового показателя

К понятию весового показателя W приводит классическая задача проверки принадлежности двух выборок одной генеральной совокупности.

Пусть имеются две выборки  и  из совокупности с функцией распределения , где  - параметр распределения, причем неизвестно, соответствуют ли выборки одному и тому же значению параметра  или - его разным значениям  и , .

Говорят, что выборки принадлежат одной генеральной совокупности, если , и - разным, если .

Проверка гипотезы  (или ) осуществляется на основе некоторого статистического критерия при альтернативной гипотезе , в качестве которой могут быть:

a)  (или  > 0), б)  (или  < 0), в)  (или   0).

Применительно к задаче учета разнородной информации при оценке надежности в качестве параметра  выступает один из показателей надежности. Например, если под  понимать вероятность безотказной работы Р изделия, а под  - биноминальный закон распределения, то придем к задаче объединения результатов испытаний по биноминальному плану, рассмотренной выше.

Стандартная процедура проверки нулевой гипотезы состоит, как известно [16, 20], в следующем:

1. Подбирается некоторая статистика Т, зависящая от выборочных наблюдений и гипотезы , распределение которой (при условии, что  верна) известно - обозначим его плотность через .

2. По заданному уровню значимости  строится критическая область    таким образом, чтобы для принятой альтернативной гипотезы  ошибка второго рода  была минимальной.

3. Наблюденное в данной выборке значение Т = Т₀ сравнивается с границей С критической области : если , то гипотеза  отклоняется на уровне значимости , если , то  принимается. При этом граница С наилучшей критической области определяется по одной из следующих формул:

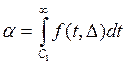, если              (3.1),

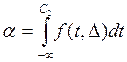, если              (3.2),

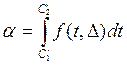, если             (3.З).

Нетрудно видеть из формул (3.1) - (3.2), что  С₁, С₂ есть квантили распределения  уровня  и  соответственно, т.e.  и  а  и  - квантили, того же распределения уровней  и .