Механика: Методические указания к практическим занятиям дисциплины "Физика"

Содержание

Введение………………………………………………………….4

1.  Кинематика…..............................................................................……..5

Основные формулы………………………………………………………5

Примеры решения задач…………………………………………………6

2.  Динамика поступательного движения ….....................................….11

Основные формулы……………………………………………………..11

Примеры решения задач………………………………………………..12

3.  Механика твёрдого тела .................................................................…20

Основные формулы……………………………………………………..20

Примеры решения задач………………………………………………..22

4.  Механические колебания и волны ....................................................29

Основные формулы……………………………………………………..29

Примеры решения задач………………………………………………..32

Список литературы……………………………………………………..38

Введение

Практические занятия являются одной из важнейших компонент учебного процесса по физике. Они способствуют приобщению студентов к самостоятельной работе, учат анализировать изучаемые физические явления, использовать на практике полученные теоретические знания.

Предназначены для студентов, изучающих раздел курса общей физики «Механика». В методических указаниях представлены примеры решения типичных задач разной степени трудности. Решения сопровождаются необходимыми примерами и комментариями. Задачи систематизированы по основным темам раздела. По каждой теме приведены основные формулы, облегчающие усвоение алгоритмов решения задач.

1. КИНЕМАТИКА

Основные формулы

Средняя скорость тела за промежуток времени Δtопределяется отношением перемещения тела Δr к промежутку времени Δt:

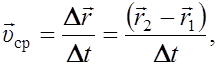
где  – радиус–вектор начальной точки,  – конечной.

Средний модуль скорости тела за промежуток времени Δt есть отношение пути S, пройденного телом за это время, к Δt:

.

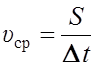Средним ускорением называется отношение изменения скорости ко времени, за которое оно произошло:

.

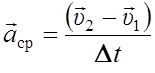Мгновенная скорость  равна производной радиус-вектора  точки по времени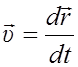                       

и направлена по касательной к траектории; для прямолинейного  движения 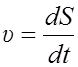                                    , ускорения                              .

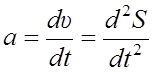Кинематические соотношения для прямолинейного равнопеременного движения:

,

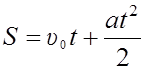, где υ₀  скорость тела в момент времени t = 0, a – ускорение тела.

При криволинейном движении полное ускорение тела раскладывается на нормальную и тангенциальную к траектории составляющие:                           .

Тангенциальная составляющая ускорения определяет изменение модуля скорости:                            ,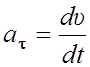

нормальная – изменение направления скорости:

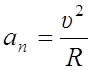, где R–радиус кривизны траектории, нормальное ускорение направлено к центру кривизны траектории.

Модуль полного ускорения:

.

При движении по окружности кинематическими характеристиками являются:

– угол поворота φ,

– угловая скорость ω = ,

– угловое ускорение ε =  = .

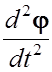Кинематические уравнения для вращательного равнопеременного движения:

ε t

φ = ω₀ t +  ε, где ω₀ – угловая скорость в момент времени t=0, e – угловое ускорение.

Линейные и угловые параметры движения связаны соотношением:                υ = ω R,a_τ = ε R.

Примеры решения задач

Задача 1

Зависимость пройденного телом пути S от времени t даётся уравнением S=A+Bt+Ct²+Dt³, где С=0,14 , D=0,01 . Через какое время после начала движения ускорение тела будет равно 1 ? Чему равно среднее ускорение тела за время от t = 0 до t = 1 ?

Решение

Мгновенное ускорение тела в момент времени t можно найти как вторую производную от пути:

a = 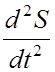 = (B+2Ct+3Dt²) = 2C+6Dt.

Надо определить значение t, при котором a= 1 .

Получим:                             t = .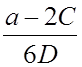

Подставив численные значения, получим:

t= 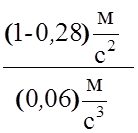 = 12 с.

Чтобы найти среднее ускорение за промежуток времени от t₁ до t₂, надо определить величины скорости в момент времени t₁ и t₂ и их разность разделить на t₂–t₁:

a_ср = .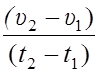

Скорость находим как производную пути по времени:

υ = B+2Ct+3Dt²,

υ₁ = B+2Ct₁+3Dt₁²,

υ₂ = B+2Ct₂+3Dt₂².

Разность скоростей:

 

υ₂ – υ₁ = 2С(t₂ – t₁) + 3D(t₂² – t₁²) = (t₂ – t₁)[2С +3D(t₂+t₁)], подставляем в формулу для среднего ускорения:

a_ср = 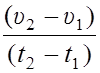 = 2С+3D(t₂+t₁).

Подставив численные значения, получим:

a_ср = 0,28 + 3^.0,01^.1с = 0,31.

Задача 2

Тело брошено со скоростью υ₀ = 14,7 , под углом α = 30^о к горизонту. Найти нормальное и тангенциальное ускорения тела через t= 1,25 с после начала движения, а также радиус кривизны траектории в данный момент времени. Сопротивление воздуха не учитывать.

Решение

Полным ускорением является ускорение свободного падения . Оно раскладывается на тангенциальную и нормальную составляющие. Если горизонтальную ось обозначить x, а вертикальную y, то g направленно по оси y, aτ – по касательной к траектории, а     an – по нормали к ней.

 

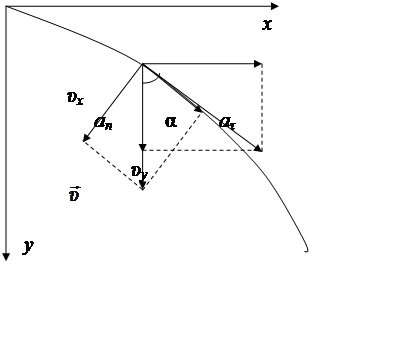
Полная скорость тела направлена по касательной к  траектории, её можно разложить на горизонтальную составляющую–υ_x и вертикальную составляющую – υ_y. Треугольники скоростей и ускорений прямоугольные и угол между υ_у и υ такой же, как и между a_τ и g (так как a_τ и υ направлены по касательной к траектории, а υ_y и        g – по оси y). Таким образом, чтобы найти a_n и a_τ, нужно определить в данный момент времени υ_x,  υ_у, υ.