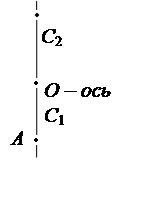Механика: Методические указания к практическим занятиям дисциплины "Физика", страница 7

            В                     которую   ему   сообщили  в  положении  А.  Если

υ – наименьшая скорость нижнего конца, при которой  он  сможет  сделать  полный  оборот, то угловая скорость стержня            w = . 

Момент инерции стержня относительно оси, проходящей через его конец, определятся по теореме Штейнера:

I =  m l² = m 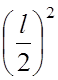 =  m l², где ml²–момент инерции стержня относительно перпендикулярной к нему оси, проходящей через центр масс,  – расстояние от центра масс до требуемой оси.

Кинетическая энергия вращательного движения:

E_k = =.= .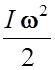

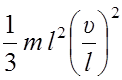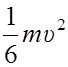По закону сохранения энергии, кинетическая энергия стержня в положении А равна его потенциальной энергии в положении В:

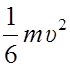 = mgl, отсюда                                 υ = .

Подставляем числовые значения:         υ = »7 м/с.

Задача 19

Человек массой m₁ = 60 кг находится на неподвижной платформе массой m = 100 кг. Какое число оборотов в минуту будет делать платформа, если человек будет двигаться по окружности радиуса 5 м вокруг оси вращения? Скорость движения человека относительно платформы равна 4 км/ч. Радиус платформы 10 м. Считать платформу однородным диском, а человека – точечной массой.

                                 Решение

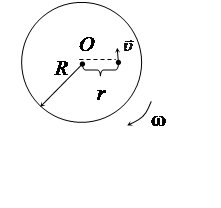 Первоначально платформа с человеком покоилась,    момент импульса этой системы был равен нулю.  Когда человек начнет двигаться по платформе,   платформа будет вращаться в противоположном  направлении. Если расстояние от человека до оси  вращения платформы r, в месте нахождения человека  u = w r.  Таким  образом,  если человек  движется относительно платформы со  скоростью

υ, то относительно земли он будет двигаться со скоростью υ – w r, его момент импульса относительно оси платформы L₁ = m₁(υ – wr)r. Момент импульса платформы относительно ее оси:

L = – Iw, где I– момент инерции платформы.

Поскольку платформа представляет собой однородный диск, то ее момент инерции относительно оси, проходящей через центр:

I = mR².

Запишем закон сохранения момента импульса для данной системы:

O = L₁ + L = m₁(υ – w r) r – mR²w, отсюда можно определить угловую скорость вращения платформы:

w = .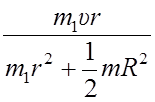

Число оборотов платформы в минуту определится из соотношения:

n = 60 =  .

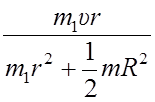Подстановка числового значений дает:

n =  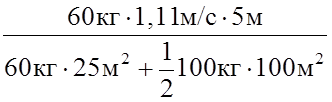 = 0,49 об/мин.

4. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ

Основные формулы

Гармонические колебания происходят по закону:

x = A cos(ωt + φ₀), где  x – смещение частицы от положения равновесия, А – амплитуда колебаний, ω – круговая частота, φ₀ – начальная фаза, t – время.

Период колебаний                       T = .

Скорость колеблющейся частицы:

υ =  = – A ω sin (ωt + φ₀), ускорение                      a =  = – Aω² cos (ωt + φ₀).

Кинетическая энергия частицы, совершающей колебательное движение:                 E_k  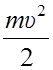=  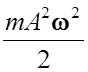=  sin²(ωt + φ₀).

Потенциальная энергия:

E_n = 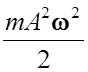 cos²(ωt + φ₀).

Периоды колебаний маятников

– пружинного                              T = 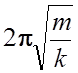, где m – масса груза, k – коэффициент жесткости пружины,

– математического                       T= 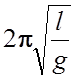, где l – длина подвеса, g – ускорение свободного падения,

– физического                             T= 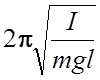, где I – момент инерции маятника относительно оси, проходящей через точку подвеса, m – масса маятника, l – расстояние от точки подвеса до центра масс.

Приведенная длина физического маятника находится из условия:                                  l_np  = , обозначения те же, что для физического маятника.

При сложении двух гармонических колебаний одной частоты и одного направления получается гармоническое колебание той же частоты с амплитудой:

A = A₁² + A₂² + 2A₁A₂ cos(φ₂ – φ₁)

и начальной фазой:             φ = arctg .

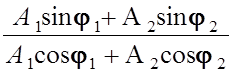где А₁, A₂ – амплитуды, φ₁, φ₂ – начальные фазы складываемых колебаний.

Траектория результирующего движения при сложении взаимноперпендикулярных колебаний одной частоты:

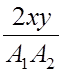 +  –  cos (φ₂  – φ₁) = sin² (φ₂ – φ₁).

Затухающие колебания происходят по закону: