Механика: Методические указания к практическим занятиям дисциплины "Физика", страница 3

Разрежем мысленно канат в месте сгиба и соединим обе части невесомой нерастяжимой нитью. Когда канат только начнёт скользить, все силы уравновесятся (так как он движется ещё без ускорения), а сила трения достигает величины силы трения скольжения,  F_тр = μΝ.

Условия равновесия сил:

mg = N

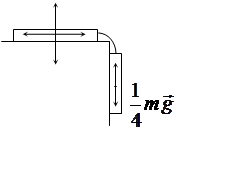F_тр = T

mg = Tm           

Отсюда:         μmg= mg, или μ =

Задача 6

 

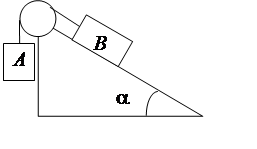                                                Решение

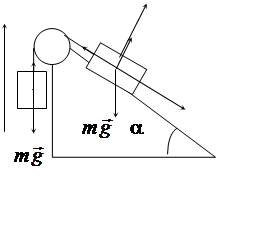   x                             y            Запишем уравнения движения обоих тел:

                                 А:  m = m +

x x                    x                            В:  m = m + +

В проекциях для тела А:

– ma=T–mg         (3)

Для тела В по оси х:

– ma = –T + mg sin a (4)

0 = N – mg cos a                (5)

Если сложить уравнения (3) и (4), то получим:

–2ma = – mg + mg sin a,или

a = g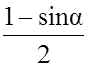

Подставив это значение, например, в уравнение (3) (можно в (4)), получаем:                        T = mg–ma = mg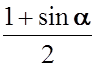

Подставляем числовые значения:

                             a = 9,8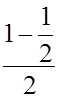 =  = 2,45

                                T = 1 ∙ 9,8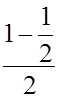 = 7,35 H

Задача7

Вагон массой 20 т, двигавшийся равномерно, под действием силы трения в 6 кН через некоторое время остановился. Начальная скорость вагона равна 54 км/ч. Найти: 1) работу сил трения;                   2) расстояние, которое вагон пройдёт до остановки.

Решение

Работа равна приращению кинетической энергии тела:

A_тр = 0 –  = – ,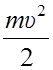

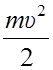Знак «–» означает, что работа сил трения отрицательна, так как силы трения направлены против движения.

С другой стороны, работу силы трения можно рассчитать через произведение силы на путь:

A_тр  =  F_тр^. S, отсюда                                      S =  =

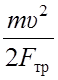
Подставив числовые значения:

m= 2^.10⁴ кг,  F_тр = 6^.10³ Н, υ = 15 , получим:

                 A_тр = 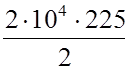 = 2,25^.10⁶ Дж = 2,25 МДж,

                                S  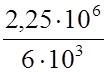=  = 358 м.

Задача 8

Камень бросили под углом α = 60^о к горизонту со скоростью υ₀=15 м/с. Найти кинетическую, потенциальную и полную энергию камня: 1) спустя одну секунду после начала движения; 2) в высшей точке траектории. Масса камня m= 0,2 кг. Сопротивлением воздуха пренебречь.

Решение

Выберем ось х – по горизонтали, а ось   у – по вертикали.   

Проекции скорости:

υ_x = υ₀cos a,(6)

    υ_о                                   υ_y = υ₀sin a – gt                                   (7)

a       x         В момент времени t модуль скорости                        определится из соотношения:

υ² = υ₀² cos² a+ (υ₀sin a – gt)² = υ₀² – 2 υ₀ gt sin a + g²t².

Высота камня над поверхностью земли в момент времени t определяется из соотношения:

         h = υ₀ sin a - .                                      (8)

Находим кинетическую, потенциальную и полную энергию в момент времени t:

E_k = 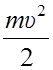 = ( υ₀² – 2 υ₀ gt sin a + g²t²),

E_п = mgh = ( 2 υ₀ gt sin a – g²t²),

E = E_k + E_п= .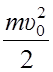

В высшей точке траектории υ_y = 0. Этой точки камень достигает за время = 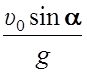(из (7)), и максимальная высота подъёма  h_max=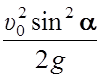 (из (8)).

E_k =  = ,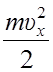

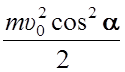E_п = mgh_max = ,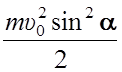

E = E_k+ E_п = .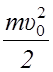

Подставляем числовые значения. В момент времени t= 1 c.

                   E_k = 17,4 Дж,    E_п = 5,1 Дж,     E = 22,5 Дж.

В высшей точке траектории:

                    E_k = 16,9 Дж,     E_п = 5,6 Дж,     E = 22,5 Дж.

Задача 9

На рельсах стоит платформа массой m₁ = 10 т, на платформе закреплено орудие массой m₂ = 5 т, из которого проводится выстрел вдоль рельсов. Масса снаряда m₃ = 100 кг, его начальная скорость относительно орудия υ₀ = 500 м/с. Определить скорость υ_x платформы в первый момент времени, если: 1) платформа стояла неподвижно,    2) платформа двигалась со скоростью υ₁ = 18км/ч, и выстрел был произведён в направлении её движения, 3) платформа двигалась со скоростью υ₁= 18 км/ч, и выстрел был произведён в направлении, противоположном её движению.

Решение