Механика: Методические указания к практическим занятиям дисциплины "Физика", страница 9

Задача 23

Точка участвует в двух колебаниях с одинаковыми периодами и начальными фазами. Амплитуды колебаний А₁ = 3 см и А₂ = 4 см. Найти амплитуду результирующего колебания, если: 1) колебания происходят в одном направлении; 2) колебания взаимно перпендикулярны.

Решение

1)  Если колебания происходят в одном направлении, то амплитуда результирующего колебания определится как:

A = , где А₁ и А₂ – амплитуды складываемых колебаний, j₁ и j₂–начальные фазы. По условию начальные фазы одинаковы, значит j₂ – j₁ = 0,       а cos 0 = 1.

Следовательно:

A = == А₁+А₂ = 7 см.

2)  Если колебания взаимно перпендикулярны, то уравнение результирующего движения будет:

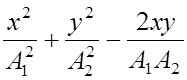cos(j ₂ – j ₁) = sin²(j ₂ – j ₁).

Так как по условию j₂ – j₁ = 0, cos 0 = 1, sin 0 = 0, то уравнение запишется в виде: 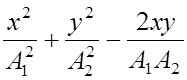                                   =0, или 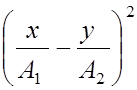                                             =0, или                                                 .

 

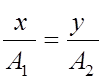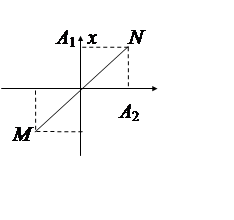Полученное соотношение между x и у можно изобразить на графике. Из графика  видно, что результирующим будет колебание точки на прямой MN.  Амплитуда этого колебания определится как:              A = = 5 см.

Задача 24

Период затухающих колебаний Т=4 с, логарифмический декремент затухания l = 1,6 , начальная фаза равна нулю. Смещение точки при t=  равно 4,5 см. 1) Написать уравнение этого колебания; 2) Построить график этого движения для двух периодов.

Решение

1)  Уравнение затухающих колебаний с нулевой начальной фазой имеет вид:                  

x = A₀e ^-bt cos2p.

Для подстановки числовых значений не хватает величин начальной амплитуды А₀ и коэффициента затухания b.

Коэффициент затухания можно определить из соотношения для логарифмического декремента затухания:            

l = bТ.

Таким образом                    b =  =  = 0,4 с^-1.

Начальную амплитуду можно определить, подставив второе условие:

4,5 см = A₀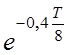cos 2p = A₀ cos  = A₀  .

Отсюда находим:

A₀ = 4,5∙ (см) = 7,75 см.

Окончательно уравнение движения:

x = 0,0775 cost.

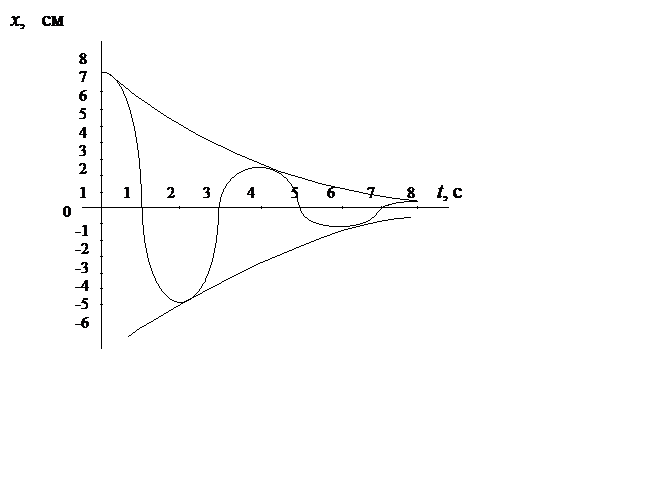
2)  Для построения графика сначала рисуем огибающую                        x = 0,0775 , а затем колебательную часть.

 

Задача 25

Чему равен логарифмический декремент затухания математического маятника, если за t= 1 мин амплитуда колебаний уменьшилась в два раза? Длина маятника l= 1 м.

Решение

Логарифмический декремент затухания можно найти из соотношения:                            l= bТ, где b – коэффициент затухания, Т – период колебаний. Собственная круговая частота математического маятника:

w₀ = 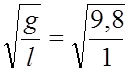 = 3,13 с^-1.

Коэффициент затухания колебаний можно определить из условия:                                       A₀ = A₀ e^-bt,

bt = ln2 = 0,693 ,

b = 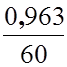 = 0,0116 c^-1.

Поскольку b << w₀, то в формуле w =  можно пренебречь b по сравнению с w₀ и период колебаний определить по формуле:                                  T =  = 2 c.

Подставляем b и Т в выражение для логарифмического декремента затухания и получаем:

l = bT = 0,0116 с^-1 ∙ 2 с = 0,0232.

Задача 26

Уравнение незатухающих колебаний дано в виде                           x = 4 sin600 pt см.

Найти смещение от положения равновесия точки, находящейся на расстоянии l = 75 см от источника колебаний, через t = 0,01 с после начала колебаний. Скорость распространения колебаний υ = 300 м/с.

Решение

Запишем уравнение волны, распространяющейся от данного источника:                     x = 0,04 sin 600 p(t – ).

Находим фазу волны в данный момент времени в данном месте:

t –  = 0,01 – 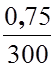 = 0,0075 ,

600p ∙ 0,0075 = 4,5p ,

sin 4,5p = sin  = 1.

Следовательно, смещение точки x = 0,04 м, т.е. на расстоянии l=75 см от источника в момент времени t = 0,01 c смещение точки максимально.

Список литературы

1.  Волькенштейн В.С. Сборник задач по общему курсу физики. – СПб.: СпецЛит, 2001.

2. Савельев И.В. Сборник вопросов и задач по общей физике. – М.: Наука, 1998.