Рассчитаем an, сократив массу
![]() = tg a, отсюда
υ =
= tg a, отсюда
υ = ![]() =41,5 м/с.
=41,5 м/с.
3. МЕХАНИКА ТВЕРДОГО ТЕЛА
Мерой инертности твердого тела при вращательном движении является момент инерции:
I= Σmi∙ ri2, где mi – элементарная масса i – го кусочка тела, ri – расстояние этого кусочка от оси вращения.
Моменты инерции некоторых твердых тел относительно оси, проходящей через их центры масс:
Полый цилиндр I = m ( R12 + R22).
Тонкий обруч I = mR2.
Сплошной цилиндр I = ![]() mR2.
mR2.
Шар I
= ![]() mR2.
mR2.
Тонкий
стержень I = ![]() ml2.
ml2.
Если ось вращения не проходит через центр масс, для расчета момента инерции используют теорему Штейнера:
I = I0 + ma2, где I – момент инерции тела относительно данной оси, I0 – момент инерции этого тела относительно оси, параллельной данной, и проходящей через центр масс, m – масса тела, а – расстояние между осями.
Основное уравнение динамики вращательного движения твердого тела: I e = M, где I – момент инерции твердого тела, относительно оси вращения, e – его угловое ускорение, М – суммарный момент сил, действующий на тело относительно данной оси.
Момент силы F равен: M = Fl, где l – расстояние от линии, вдоль которой действует сила, до оси вращения.
Момент импульса твердого тела относительно неподвижной оси: L = Iω, где I – момент инерции твердого тела относительно данной оси, ω – угловая скорость его вращения.
Момент импульса материальной точки относительно неподвижной оси: L = mυr, где m – масса частицы, υ – ее скорость, r – расстояние от линии, вдоль которой движется частица, до данной оси.
В замкнутой системе частиц полный момент импульса не меняется: ΣLi = const.
Кинетическая энергия вращающегося тела:
Ek = 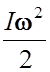 , где I – момент инерции тела, ω – его угловая скорость.
, где I – момент инерции тела, ω – его угловая скорость.
Кинетическая энергия катящегося тела:
Ek = 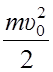 +
+ 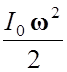 , где m – масса тела, υ0 – скорость
поступательного движения центра масс, I0 – момент инерции тела
относительно оси, проходящей через центр масс, ω – угловая
скорость вращения тела.
, где m – масса тела, υ0 – скорость
поступательного движения центра масс, I0 – момент инерции тела
относительно оси, проходящей через центр масс, ω – угловая
скорость вращения тела.
Примеры решения задач
Задача 13
Прямой круглый однородный конус имеет массу m и радиус основания R. Найти момент инерции конуса относительно его оси.
Решение
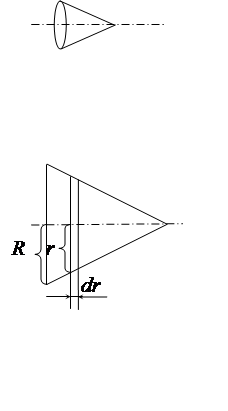 Разобьём конус
на цилиндрические слои ось толщиной dr. Масса такого
слоя
Разобьём конус
на цилиндрические слои ось толщиной dr. Масса такого
слоя
dm = rpr2dr, где ρ – плотность материала, из которого изготовлен конус. Момент инерции этого слоя
dI = dm.r2.
Момент инерции всего конуса складывается из моментов инерции всех слоёв:
I
= ![]() =
= ![]() ρπ r 4 dr =
ρπ r 4 dr = ![]() ρR5.
ρR5.
Остаётся выразить его через массу всего цилиндра:
m = 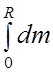 =
=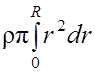 =
=![]() R3, отсюда
ρ =
R3, отсюда
ρ = 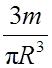 ,
,
I = 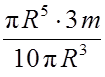 =
= ![]() mR2.
mR2.
Задача 14
Маховое колесо, имеющее момент инерции 245 кг∙м2, вращается с частотой 20 об/с. Через минуту после того, как на колесо перестал действовать вращающий момент, оно остановилось. Найти: 1) момент сил трения; 2) число оборотов, которое сделало колесо до полной остановки после прекращения действия сил.
Решение
При торможении угловое ускорение отрицательно. Найдём его модуль из кинематического соотношения для угловой скорости.
ω 0 = 2 π ν0, ω = 0,
0 = 2 π ν0 - ε t, отсюда
ε
= 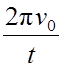 .
.
Это ускорение обусловлено действием момента сил трения
Mтр = I ε = 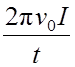 .
.
Полный угол поворота при равнозамедленном движении находится из соотношения:
φ = ω0
t- ![]() ,
,
φ =2π N, ω 0
= 2
π ν0, ε = 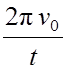 .
.
Перепишем соотношения для угла в виде:
2π N = 2 π ν0 t - ![]() = 2 π ν0 t -
= 2 π ν0 t - 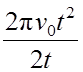 =
= 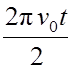 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.