Механика: Методические указания к практическим занятиям дисциплины "Физика", страница 6

Для нахождения числа оборотов получим:

N = .

Подставив числовые значения, найдём:

M_тр = 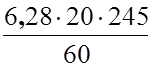 = 506 Нм,

N = 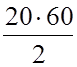 = 600 об.

Задача 15

На барабан радиусом R= 20 см, момент инерции которого равен I= 0,1 кг∙м², намотан шнур, к которому привязан груз массой             m= 0,5 кг. До начала вращения высота груза над полом равна h₁ = 1 м. Найти: 1) через какое время груз опустился до пола; 2) кинетическую энергию груза в момент удара о пол; 3) натяжение нити. Трением пренебречь.

                                    Решение

R                   T                     T          m                        h1

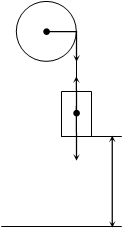На груз действует сила тяжести mg и сила натяжения шнура Т. Уравнение поступательного          движения груза             ma = mg – T.

Барабан вращается вокруг неподвижной оси. Его уравнение движения               M = I ε, где М – момент силы натяжения шнура, М = TR,                                                I – момент  инерции барабана,ε =  – его угловое ускорение.

TR = I .

Выражаем отсюда силу  натяжения шнура:

           T = I                                               (10)

и подставляем ее в уравнение движения груза:

mg = a(m + ) = am(1 + ).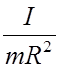

Получаем ускорение груза:

         a = 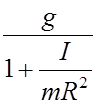.                                               (11)

Время движения груза можно найти из уравнения:

                                                   h₁ = ,

t =  = .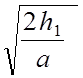

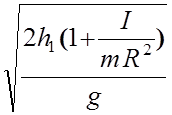В момент удара о пол груз имел скорость:

                      υ = at = .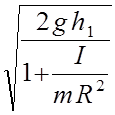

Следовательно, его кинетическая энергия:

                   E_k = =.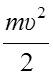

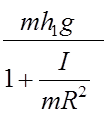Подставив выражение для ускорения (11) в формулу (10), получим:                          T = = .

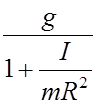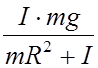Подставив числовые значения, определим искомые величины:

                                  t = 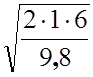 = 1,1 c,

       E_k = 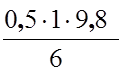 = 0,82 Дж,

T = 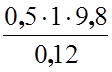 = 4,1 Н.

Задача 16

Шар массой m = 1 кг, катящийся без скольжения, ударяется о стенку и откатывается от нее. Скорость шара до удара о стенку           υ = 10 см/с, после удара 8 см/с. Найти количество тепла Q, выделившееся при ударе.

Решение

Кинетическая энергия катящегося тела равна:

                       E_k = 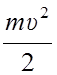+ 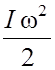.                                         (12)

Момент инерции шара                I = 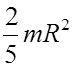, угловая скорость вращения            w = .

Подставляем эти величины в формулу (12):

E_k = 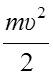+  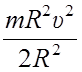=  m υ ².

Количество тепла, выделившегося при ударе, равно разнице его кинетических энергий до и после удара:

Q = E_k1 – E_k2 = m υ₁² - m υ₂² = m(υ₁² - υ₂²).

Подставив числовые значения, получим:

  а = ∙1(100∙10^-4 – 64^.10^-4) = 10^-4 = 2,25∙10^-3 Дж = 2,52 МДж.

Задача 17

Найти кинетическую энергию велосипеда, едущего со скоростью υ = 9 км/ч. Масса велосипедиста вместе с велосипедом     m = 78 кг, причем на колеса приходится масса m₁ = 3 кг. Колеса считать тонкими обручами.

Решение

Кинетическая энергия велосипеда складывается из кинетической энергии поступательного движения и кинетической энергии вращательного движения колес.

E_k =  + .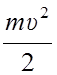

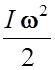Момент  инерции колес, представляющих собой тонкие обручи, равен I = , а угловая скорость вращения w = .

Подставляем эти значения в выражение для кинетической энергии:                        E_k =  +  = .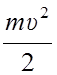

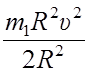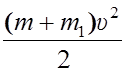Скорость надо перевести в м/с: υ = 2,5 м/с.

Подстановка числовых значений дает: E_k =253 Дж.

Задача 18

Однородный стержень длиной 85см подвешен на горизонтальной оси, проходящей через верхний конец стержня. Какую наименьшую скорость надо сообщить нижнему концу стержня, чтобы он сделал полный оборот вокруг оси?

Решение

Чтобы стержень смог сделать полный оборот вокруг оси, он должен подняться до вертикального положения В.

Если отсчитывать потенциальную энергию стержня от начального положения А, то в положении В центр масс его поднят  на высоту С₂-С₁=l – длина стержня. Стержень приобретает потенциальную   энергию  Е_n = mgℓ  за   счет   кинетической   энергии,