1. Система отсчета. Траектория, путь и перемещение.
Система отсчета состоит из 3-х компонентов:
а) материальная система координат;
б) тело отчета (связано с началом);
в) способ отчета времени (часы).
Мат. точка – тело, размерами кот. можно пренебречь в условиях данной задачи.
Твердое тело – тело, деформациями кот. в данных условиях можно пренебречь.
Траектория – линия, которую описывает в пространстве материальная точка при своем движении.
Движение бывает прямолинейным и криволинейным.
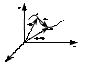
Радиус-вектор – вектор, проведенный от начала сис-мы отсчета к данной материальной точке.
![]() – закон
движения
– закон
движения
Вектор перемещения – вектор, проведен. из т. начала в т., где тело оказалось в последний момент времени.
Путь – длина участка траектории (скалярная, положит. велич.).
2. Векторы и действия над ними.
Вектор – отрезок прямой, характер. длиной и напр.
1)
![]()
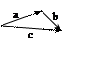
2)
![]()
![]()
3)
![]()
![]()
4)
![]()
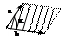
5)
![]()
![]()
a) ![]()
b) ![]()
c) против часовой
по часовой ¯
![]() – «правая тройка»
– «правая тройка»
6)
![]()
Любой вектор можно представить в виде n векторов.
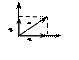
![]()
![]() – составл. вектора a по
оси Ox
– составл. вектора a по
оси Ox
ax – проекция вектора a на ось Ox
![]()
![]()
![]()
![]()
![]()
3. Скорость и ускорение как производные радиус-вектора по времени.
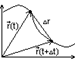 Мгновенная скорость – отношение
б.м. перемещения к б.м. промежутку времени, за которое это перемещение
совершено.
Мгновенная скорость – отношение
б.м. перемещения к б.м. промежутку времени, за которое это перемещение
совершено.
![]()
![]() – производная от радиус-вектора по времени
– производная от радиус-вектора по времени
![]()
![]()
![]()
Ускорение – быстрота изм. скорости.
![]()
![]()
Ускорение – отн. б.м. приращения к б.м. промежутку времени, за кот. произошло это приращение; – это производная от мгновенной скорости по времени.
![]()
Ускорение – вторая производная от радиус-вектора по времени.
4. Равномерное и равнопеременное движ.
I. Прямолинейное равномерное движение – это движение при котором тело за любые равные промежутки времени совершает равные перемещения.
![]()
![]()
![]()
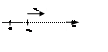 tg
a=vx
tg
a=vx
ax=0; x0=x(0);
vx=const=v; x=x0+Vxt
II. Равнопеременное движение. Прямолинейное.
ax=const; tg a=ax
![]()
![]()
![]() vx=v0x+axt;
vx=v0x+axt;
![]()
5. Угловая скорость и ее связь с линейной скоростью.
Плоское – движение, происходит в одной плоскости.
Поступательное – движение тв. тела, при кот. прямая, проведенная через 2 любые т. тв. тела, остается ║ самой себе (св-во: все точки тв. тела в данный момент времени имеют одинаковую скорость, поэтому поступательное движение ~ движению м.т.)
Вращательное движение – все т. тв. тела описывают окружности, центры кот. лежат на одной прямой.
Скорость точек при вращательном движении в любой момент времени различны.
При описании вращ. движ. направление поворота удобно характеризовать углом Dj, кот. мы будем рассм. как вектор.
Dr=R×Dj
R=r×sin a
![]()
Dr=Dj×r×sin a=Dj×R
![]()
![]()
![]()
Угловая скорость – отн. б.м. угла поворота к б.м. промежутку времени, за кот. произошел этот поворот.
6. Нормальное, тангенциальное и угловое ускорения.
При плоском движении векторы скорости и ускорения как правило не совпадают по направлению.
![]()
![]()
Тангенциальное ускорение – составляющее ускорения, совпадает с напр. скорости (aτ=acosα).
Нормальное ускорение – составляет со скорость угол 90º
![]()
![]()
![]()
Физ. смысл: Тангенциальное ускорение характеризует изменение модуля скорости. Нормальное ускорение характеризует изменение направления скорости.
Замечание. При движении по окружности нормальное ускорение иногда называют центростремительное.
![]()
Угловое ускорение – отношение б.м. приращения угловой скорости к б.м. промежутку времени.
![]()
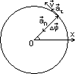
7. Равномерное и равнопеременное движение по окружности.
а) равномерное движение
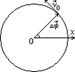
![]() ; ω=const=ω0;
; ω=const=ω0;
aτ=0 ; ε=0; φ=φ0+ω0t
![]() ;
;![]()
б) равномерное движение
![]() ;
;![]()
![]()
![]()
![]()
![]()
равноускоренное движ. – ![]()
равнозамедленное движ. – ![]()
8. Связь между угловыми и линейными величинами ускорений в случае вращения тела вокруг своей оси.
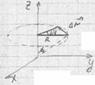
![]() ;
;![]()
![]() ;
;![]()
![]() ;
;![]()
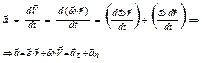
![]() ;
;![]() ;
;![]()
![]() ;
; ![]()
более общий случай
![]()
![]()
![]() .
.
9. Закон инерции и инерциальные системы отсчета. Преобразования Галилея.
I закон Ньютона: тело находится в состоянии покоя или прямолинейного равномерного движения, если на него не действует другие тела или действие других тел скомпенсировано.
Системы отсчета, в которых выполняется I закон Ньютона называется инерциальными (ИСО).
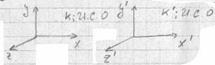 Любая
СО, кот. движется прямолинейно и равномерно относительно ИСО тоже является ИСО
Любая
СО, кот. движется прямолинейно и равномерно относительно ИСО тоже является ИСО
пусть K' движется относительно K с V=const, по Ох
Координаты связаны следующим отношением:
![]() x` - координата тела в K`: ИСО
x` - координата тела в K`: ИСО
это преобразования Галилея для координат
![]() преобразование Галилея для скорости
преобразование Галилея для скорости
![]() - преобразование для ускорения
- преобразование для ускорения
Все законы механики имеют один и тот же вид во всех ИСО - принцип относительности Галилея.
Состояние покоя и равномерное прямолинейное движение одно и то же.
10. Масса. Сила. II и III законы Ньютона.
II закон Ньютона: произведение массы тела на его ускорение равно результирующей всех сил действующих на тело.
![]()
II з-н Ньютона выполняется только в ИСО.
Любое тело противится попыткам изм. характер его движ. Это св-во тел называется инертностью. Масса – мера инертности.
Масса явл. внутр. хар-кой тела. Масса – величина аддитивная.
Сила – мера взаимодействия тел. Вектор.
II закон Ньютона содержит утверждения:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.