Ответы на экзаменационные вопросы № 1-34 по разделу "Механика" дисциплины "Физика" (Система отсчета. Траектория, путь и перемещение. Плотность потока энергии волны. Стоячие волны), страница 3

Λ=βT– логарифмический декремент затухания

 – число колебаний за время, в теч. кот. амплитуда уменьшилась в e раз

Добротность: ,                     где Q,Λ – безразмерные

В случае сильного затухания (ω₀≤β):

23. Законы изменения и сохранения полной механической энергии системы  м. т.

а) закон сохр. полной мех. энергии замкнутой сис-мы мат. т., в кот. действ только консервативные силы.

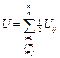
                              A₁₂=U₁-U₂

A₁₂=W₂-W₁

 

U₁-U₂= W₂-W₁

U₁+ W₁=U₂+W₂=const                    E₁=E₂

полн. механич. энергия замкнутой системы мат. т., в кот. действ. только консерв. силы, сохраняется.

б) закон изменения

                                      просуммируем

                   по i

работа сил трения + работа внешних сил над системой равны изменению полн. мех. энергии системы мат. т.

24. Законы сохранения для абсолютно упругого и неупр. ударов.

1)абсолютно упругий:

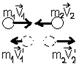удар, при кот. выполн. след. законы:

называется абсол. упругим ударом

2)абсолютно неупругий:

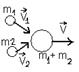удар, при кот. выполняется закон:

называется абсолютно неупругим ударом.

25. Гармонические колебания. Дифференц. уравнения гармонических колебаний.

Движение, при котором тело периодически отклоняется от положения равновесия, называется колебанием.

F_x=-kx;;ma_x=F_x ;;

;;

 – диффер. ур-е гармонических колебаний

, A, j - произвольные

гармонические – колебания, происходящие по закону cos или sin

А – амплитуда (max откл. от положения равновесия)

j – начальная фаза

 – фаза колебания,

Т – период колебания (min промежуток времени, через кот. колебание повторяется)

- частота                              

- собственная частота (круговая)

27. Сложение гармонич. колебаний одного направл. и одинаковой частоты. Биения.

метод векторных диаграмм:

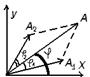
(t = 0)

Биение.

Частоты немного отличны.

;

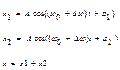Амплитуды одинаковы

26. Энергия гармонических колебаний. Математический маятник.

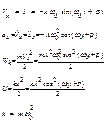
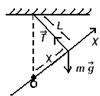математич. маятник – мат. т., подвешенная на невесомой нерастяжимой нити.

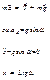
при малых углах (a<20°)

;

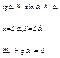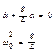
решение:

28. Сложение взаимно-перпендикулярных гармонич. колебаний. Фигуры Лиссажу.

1)

;;

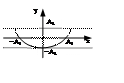
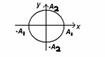если частоты колебаний равны, то при сложении 2-х взаимно-перпенд-х колебаний его траектория – эллипс

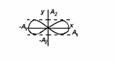2)

3)

4)

               ¥

              

               µ

29. Дифф-ное ур-ие затух. колебаний.

;

;

;  – коэффициент затухания

 – собственная частота

Дифф. ур-е затухающих колебаний:

ω₀>β – затухание не слишком велико

x=Ae^-βtcos(ωt+φ)                              A,φ – произвольные

Частота затухающих колебаний:

A(t)=Ae^-βt                                         

31. Дифф-ное ур-ие вынужд. колебаний.

Вынужденные – колебания, кот. происходят в колеб. системе под действием периодической вынуждающей силы.

;

т.к. ;;, то  – дифф. ур-е вынужд. колебаний

(любых)

x=A(ω)cos(ωt–φ(ω))                                                     

A(ω) – амплитуда φ(ω) – начальная фаза

–

определены частотой вынужденных колебаний

– время, за которое колебание установится

32. Амплитуда вынужд. колеб. Резонанс.

;

амплитуда                          нач. фаза колебаний

Резонанс – частота, при кот. амплитуда вынужденных колебаний стремиться достичь максимума. Это явление резкого увеличения амплитуды вынужденных колебаний при приближении частоты внешней периодической силы к резонансной.

резонансная частота:

1)

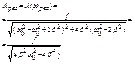
 (при ω₀>>β)

2) β→0

(разрушается)

при резонансе колебания системы отстают по фазе на π/2 от вынуждающей силы.

33. Продольные и поперечные волны в упругой среде. Ур-ие бегущей волны.

Волны: а) продольные – направление колебаний частиц в среде совпадает с направление волны (звук).

б) поперечные – колебание частиц в среде происходит в направлении ^ направлению распространения волны.

В среде могут одновременно распространяться как продольные, так и поперечные волны.

x(y,t)=Acos(ωt–φ(y))

φ(y)=ky; k – волновое число

Ур-е стоячей волны:

по оси слева направо:

x(y,t)=Acos(ωt–ky)

по оси справа налево:

x(y,t)=Acos(ωt+ky)

T – min промежуток времени, через которое колебания частиц воды полностью повторяется.

w(t+T)–ky=ωt–ky+2π

ωT=2π

ωt–k(y+x)=ωt–ky–2π

kx=2π

 – длина волны

λ=vT (v – скорость распространения волны)

34. Плотность потока энергии волны. Стоячие волны.

Распространение волны в упругой среде сопровождается переносом энергии.

Рассчитаем энергию, кот. переносится волной через ^ площадку S` за время ∆t:

за время ∆t все частицы внутри параллелепипеда придут в движение

E_кол – полная энергия колебания 1 частицы

x=Acos(ω₀t+φ); 

V_max=Aω₀             ρ=nm

;                    

Плотность потока энергии – энергия, кот. переносится в упругой среде в ед. времени через единичную верт. площадку.

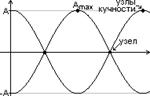
Стоячие волны.

Рассмотрим одновременно распространение 2-х волн с одинаковой частотой и амплитудой навстречу друг другу.

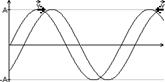Каждая волна переносит E, но одна ®, а другая ¬; т.к. амплитуды и частоты одинаковы, то перенос через площадку E=0.

x₁=Acos(ωt–ky)

x₂=Acos(ωt+ky)

x_рез=x₁+x₂=Acos(ωt–y)+Acos(ωt+ky)=2Acos(ky)cos(ωt)=A(y)cosωt