а) силы действ. на тело независимы друг от друга;
б) силы действуют попарно (следствие из III з-на Ньютона).
III закон Ньютона: тела взаимодействуют силами равными по величине и противоположными по напр.
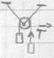Силы фигурирующие в III
з-не Ньютона приложены к разным телам и не уничтожают друг друга.
11. З-н измен. импульса матер. точки.
;
; m=const
;
– импульс;
– еще один вид II закона Ньютона
– закон
изменения импульса
–
импульс силы
Закон изменения импульса: изм. импульса мат. точки равно импульсу силы, действ. на данную мат. точку.
12. З-ны изм. и сохр. импульса сис. мат. т.
Силы, с кот. взаимодействуют мат. точки называются внутренними. Внешние силы – силы, кот. действуют со стороны тел не входящих в систему.
Исп. II з-н Н. для каждой м.т. входящей в систему:
;
векторная сумма всех внутренних сил равна нулю
–
импульс системы мат. точек.
Импульсом системы мат. точек является векторная сумма этих мат. точек.
–з-н изм. импульса системы мат. точек
Производная по времени от импульса сис-мы м.т. равна векторн. сумме внешн. сил, действ. на сис-му.
Если
, то 
Когда
, то сис-ма мат. точек называется
замкнутой.
Импульс замкнутой системы материальных точек со временем не изменяется (сохраняется).
13. Центр масс системы материальных точек и закон его движения.
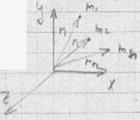Центром масс системы мат.
точек называется точка в пространстве, координаты кот. описыв. ур-ием:
,
;
;
;
для замкнутой системы 
Центр масс замкнутой системы мат. точек движется прямолинейно и равномерно.
;
– закон
движ. центра масс.
Центр масс сис-мы м.т. движется таким образом, как если бы вся масса сис-мы была сосредоточена в этой т. и все внешние силы, действ. на систему, были бы приложены к этой т.
14. Силы в механике.
1) Сила тяжести (Fтяж), при H<<RЗемли
Направлена вертикально вниз.
2) Гравитационная сила
З-н всемирного тяготения: две мат. точки притягиваются друг к другу силой, прямо пропорциальной произведению их масс и обратно пропорциальной квадрату расстояния между ними.
3)
Сила упругости Fx=-kx, где х - отклонение
пружины от состояния равновесия, k - коэффициент упругости.
4) Сила реакции опоры
N ^ поверхности, N= -N1
5) Cила натяжения нити
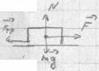
6) Cила сухого трения
– если
тело движется
– если
тело покоится
7)сила вязкого трения (в жидкости)
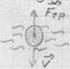
– для
малых скоростей.
15. Работа переменной силы. Мощность.
–
элем. работа
Дифференциал элементарной работы называют скалярное произведение силы на расстояние.
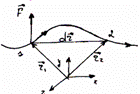
Мощностью(N) - называют отношение элементарной работы к промежутку времени, в течении которого была совершена эта работа.
; Nцентростремительное=0
16. Кинетическая энергия мат. точки и её связь с работой результирующей всех сил.
;
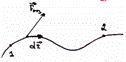
– кинетическая энергия м.т.
W2-W1=A12
Теорема о кинетической энергии: изменение кинетической энергии тела равно работе результирующей всех сил, действующих на тело.
dW=dA – Дифференциал кинетической энергии тела равен элементарной работе результирующих всех сил, действующих на тело.
17. Кинетическая энергия сис-мы м.т. и её связь с работой внешних и внутр. сил.
–
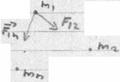
кинет. энергия системы мат. точек
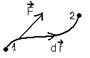Дифференциал
кинетической энергии системы мат. точек равен элементарной работе внутренних и
внешних сил, действующих на систему.
– т. о кинет. энергии системы мат. т.
Изменение кинетической энергии системы мат. точек равно работе внутр. и внешн. сил, действ. на тело.
18. Потенциальная энергия м. т. в поле сил и её связь с работой консервативных сил.
Если в каждой точке пространства на тело действует сила, то говорят, что тело находится в поле сил.
а) однородное поле сил 
(
);
б) центростремительное
Поле сил назыв. стационарным, если силы явно от времени не зависят.
Если работа по перемещению мат. точки из т.1 в т.2 не зависит от формы траектории, то такие силы называется консервативными. Для консервативных сил вводится потенциальная энергии.
dA=-dU
Элементарная работа консервативных силы равна минус дифференциал потенциальной энергии.
; 
19. Потенциальная энергия материальной точки в однородном поле тяжести.
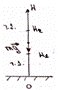
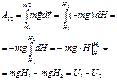
U=mgh – потенциальная энергия
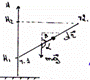
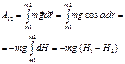
20. Потенциальная энергия матер. точки в центральном гравитационном поле.
; 
;
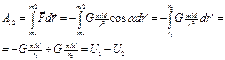
21. Потенц. энергия силы упругости.
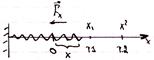
Fx=-kx
k – жесткость пружины, x – отклон. от положения равновесия.
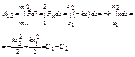Þ
22. Законы изменения и сохранения полной механической энергии матер. точки.
а) закон сохранения:
по теории о кинетич. энергии
W2-W1=A12
U1-U2=W2-W1
U1+W1=U2+W2=const E=U+W
E1=E2=const полн. мех. энергия
Если мат. точка движется в поле консервативных сил, то ее полн. мех. энергия сохраняется.
б) закон изменения:
сила трения – диссипативная сила
по теореме о кинетической энергии
A12=W2-W1
изменение полн. мех. энергии равно работе сил трения
30. Характер-ки затухающих колебаний.
Время, за кот. амплитуда затух.
колебаний уменьшится в e раз обратно β (β обратен времени τ, за
кот. A уменьшится в e раз) 
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.