Улучшение эксплуатационных характеристик гидропривода колесного хода, страница 17

Исходя из заданного диаметра и стремления обеспечить наибольшую критическую скорость останавливаемся на витке со следующими данными (номер пружины 305): ; ; ; жесткость одного витка ; наибольший прогиб одного витка .

Учитывая, что пружина II класса норма напряжений  (табл.2, т.3, [2]), находим, что для найденного диаметра проволоки расчетное напряжение .

Принадлежность ко ІI классу проверяем путем определения отношения , для чего предварительно находим критическую скорость по формуле (3), с.104, табл.10, при :

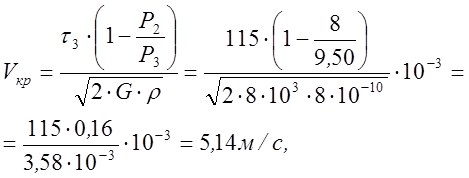                      (12.2)

где  - модуль сдвига; .

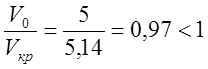.                                            (12.3)

Полученная величина свидетельствует про отсутствие соударения витков, и, следовательно, выбранная пружина удовлетворяет заданным условиям; но так как пружина ІІ класса относится к разряду ограниченной выносливости, то следует учитывать комплектацию машины запасными пружинами с учетом опытных данных.

Жесткость пружины

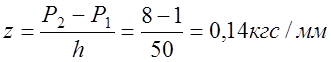.                        (12.4)

Число рабочих витков пружины

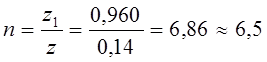.                                   (12.5)

Уточненная жесткость

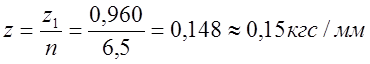.                           (12.6)

При полутора нерабочих витках полное число витков

,                                       (12.7)

где - число опорных витков.

Средний диаметр пружины

.                            (12.8)

Вычисляем деформации, высоты и шаг пружины:

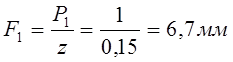;                                                  (12.9)

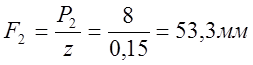;                                     (12.10)

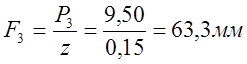;                                      (12.11)

,              (12.12)

где  - число зашлифованных витков;

;                             (12.13)

;                               (12.14)

;                          (12.15)

.                             (12.16)

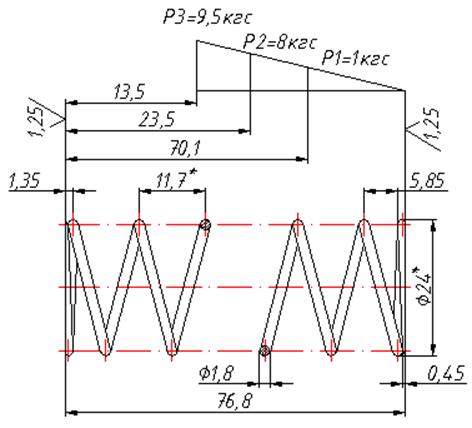
Рис.12.1.Пружина сжатия для гидроцилиндра

Пружина правильно подобрана, поскольку есть запас на несоударяемость витков.

12.2.Расчет основных размеров обратного клапана (МА91.18.ДП.41.000.СБ)

Определяем площадь щели клапана (рис.12.3) по формуле, мм:

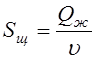,                                                     (12.17)

где  - расход жидкости (воды);  - средняя скорость движения жидкости в клапане (задаемся).

.

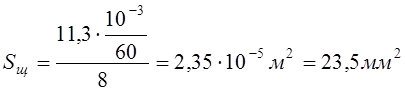Определим высоту подъема затвора клапана, мм:

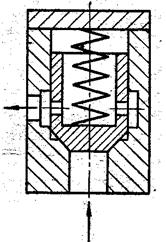
Рис.12.2.Схема гидроклапана давления с коническим седлом

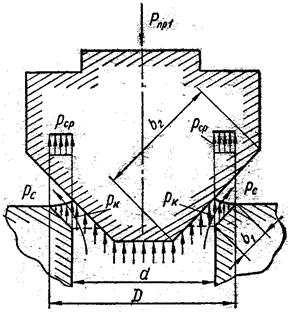
Рис.12.3.Расчетная схема гидроклапана с коническим седлом

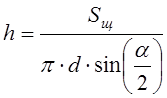,                                         (12.18)

где  - внутренний диаметр седла клапана (задаемся);

 - угол конусности, чтобы затвор не заклинивало, принимают , конструктивно примем .

.

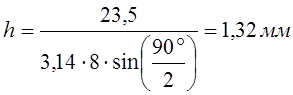Минимальная ширина седла  конического клапана должна быть не менее 0,25мм. Конструктивно принимаем ширину седла , а ширину конуса

Определим диаметр затвора седла из  отношения .

Подставив значения в формулу, получим , примем по ГОСТ 12447-80 .

Рассчитаем усилие, действующее на пружину, кгс:

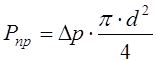,                                           (12.19)

где  - перепад давления на обратном клапане.

.

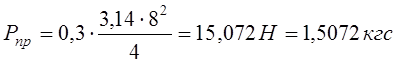12.2.1.Расчет пружины сжатия для обратного клапана

(МА91.18 ДП.41.004)

Задаемся такими размерами:

·  Сила пружины при предварительной деформации

·  Сила пружины при рабочей деформации ;

·  Рабочий ход ;

·  Наружный диаметр пружины ;

·  Наибольшая скорость перемещения подвижного конца пружины при нагрузке или разгрузке ;

·  Стойкость – число циклов до разрушения .

При заданной стойкости пружину относим ко II классу (табл.1, т.3, [2]).

По формуле (12.20) (табл.10, т.3, [2]), пользуясь интервалом значений  формулы 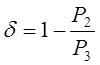1 (табл.10, т.3, [2]), находим граничные значения силы :

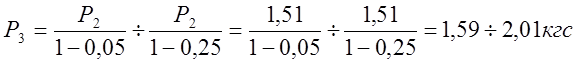.             (12.20)

В интервале от 1,59 до 2,01 кгс (табл.15, т.3, [2]) имеются такие силы : 1,60 и 1,80 кгс.

Исходя из заданного диаметра и стремления обеспечить наибольшую критическую скорость останавливаемся на витке со следующими данными (номер пружины 191): ;; ; жесткость одного витка ; наибольший прогиб одного витка .

Учитывая, что пружина II класса норма напряжений  (табл.2, т.3, [2]), находим, что для найденного диаметра проволоки расчетное напряжение .

Принадлежность ко ІI классу проверяем путем определения отношения , для чего предварительно находим критическую скорость по формуле (12.21) (табл.10, [2]), при :

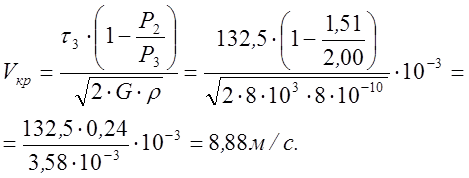            (12.21)