2 Лабораторная работа №1
Методика снятия временных и частотных характеристик линейных динамических систем. Типовые воздействия
2.1 Цель лабораторной работы
Целью данной лабораторной работы является освоение методики исследования линейных динамических звеньев и систем с помощью пакетов прикладных программ Simulink, Power System Blockset, LTI Viewer системы MATLAB.
2.2 Теоретическая подготовка
Изучите гл. 3 (с.54-56) и п. 1.3 (с. 28-31) соответственно в [1] и [2]. Особое внимание обратите на то, что характер процесса управления зависит как от структуры и параметров самой автоматической системы, так и от вида внешних воздействий и места их приложения. Ознакомьтесь с математическим описанием типовых внешних воздействий.
В данной лабораторной
работе будут рассмотрены наиболее часто используемые типовые воздействия:
единичная ступенчатая функция ![]() - функция
Хевисайда, единичный импульс
- функция
Хевисайда, единичный импульс ![]() - функция
Дирака , линейно-изменяющееся воздействие
- функция
Дирака , линейно-изменяющееся воздействие ![]() и
гармоническое воздействие
и
гармоническое воздействие ![]() . Важной
особенностью данных типовых воздействий является то, что они имеют нулевое
значение при
. Важной
особенностью данных типовых воздействий является то, что они имеют нулевое
значение при ![]() .
.
Единичная ступенчатая функция описывается следующей зависимостью:
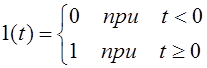 , (2.1)
, (2.1)
и имеет вид, представленный на рис. 2.1,а.
Если ступенчатое воздействие возникает в момент времени, отличный от нуля, как это показано на рис.2.1,б, то такая функция описывается уравнением:
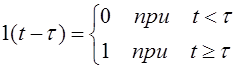 . (2.2)
. (2.2)
Дельта-функция Дирака - ![]() имеет
следующее математическое описание:
имеет
следующее математическое описание:
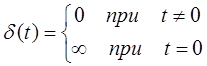 . (2.3)
. (2.3)
Таким образом, это импульс с бесконечной амплитудой, площадь которого принимается равной 1, т.е.
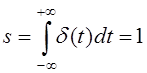 . (2.4)
. (2.4)
 |
Для автоматических систем является менее распространенным видом входного воздействия, чем единичная ступенчатая функция. Однако для теоретического описания последних имеет существенное значение.
Единичная ступенчатая
функция ![]() легка для практической реализации с
высокой точностью, однако дельта-функцию Дирака
легка для практической реализации с
высокой точностью, однако дельта-функцию Дирака ![]() реализовать
сложнее. Для практического исследования систем и их моделирования ее можно
грубо представить с помощью двух ступенчатых функций:
реализовать
сложнее. Для практического исследования систем и их моделирования ее можно
грубо представить с помощью двух ступенчатых функций:
![]() , (2.5)
, (2.5)
где: ![]() - реальный импульс;
- реальный импульс;
![]() -
амплитуда функций (
-
амплитуда функций (![]() );
);
![]() -
время, на которое запаздывает вторая ступенчатая функция (
-
время, на которое запаздывает вторая ступенчатая функция (![]() ).
).
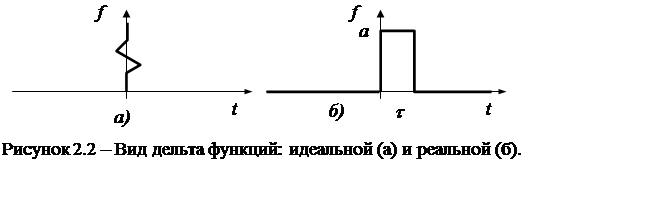 |
Как видно из рис. 2.2,б, площадь реального импульса будет равняться:
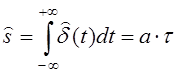 . (2.6)
. (2.6)
В соответствии с (2.4) и (2.6)
реакции линейных динамических звеньев (систем) на реальный и идеальный скачки
будут отличатся в масштабе ![]() равном:
равном:
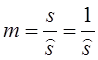 . (2.7)
. (2.7)
При выборе амплитуды и длительности
реального импульса руководствуются техническими характеристиками исследуемой
системы. Например, для электрической цепи амплитуда импульса ![]() должна быть несколько меньшей или
равной предельно допустимому напряжению для данной цепи. Длительность импульса
должна быть несколько меньшей или
равной предельно допустимому напряжению для данной цепи. Длительность импульса ![]() , как правило, выбирают на 1-2
порядка меньшей самой малой постоянной времени исследуемой системы.
, как правило, выбирают на 1-2
порядка меньшей самой малой постоянной времени исследуемой системы.
Единичные ступенчатые (2.1)
и (2.2) функции можно рассматривать как "функции-включатели". Чтобы
задать момент времени ![]() включения некоторой
произвольной функции
включения некоторой
произвольной функции ![]() достаточно ее домножить на
единичную ступенчатую функцию, т.е.
достаточно ее домножить на
единичную ступенчатую функцию, т.е.
![]() . (2.8)
. (2.8)
Выражение (2.8) служит
основой для получения таких типовых воздействий как скачек амплитудой ![]() (при
(при ![]() ),
типовое линейно-изменяющееся воздействие (при
),
типовое линейно-изменяющееся воздействие (при ![]() ,
, ![]() - скорость изменения сигнала), типовое
гармоническое воздействие (при
- скорость изменения сигнала), типовое
гармоническое воздействие (при ![]() ).
).
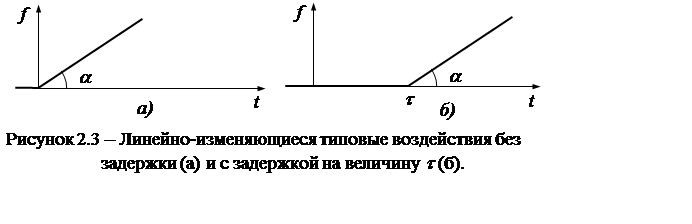
Линейно-изменяющееся воздействие (рис. 2.3,а) описывается следующей зависимостью:
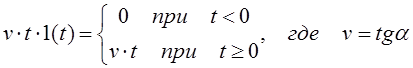 , (2.9)
, (2.9)
Линейно-изменяющееся воздействие, возникающее в момент времени t (рис. 2.3 б), описывается как:
 |
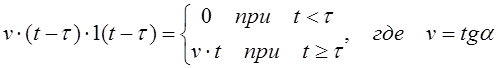 , (2.10)
, (2.10)
Формула общей зависимости, описывающая типовое гармоническое воздействие следующая:
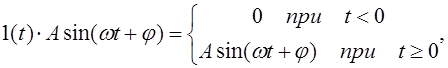 (2.11)
(2.11)
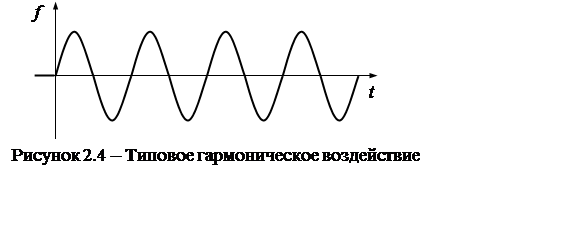 |
Типовые воздействия (2.1)-(2.3), (2.5), (2.9), (2.10) позволяют получить переходные (временные) характеристики звена (системы), а воздействия типа (2.11) – частотные характеристики. Следует заметить, что данные характеристики дают исчерпывающее описание динамических и статических свойств звена (системы).
В данной лабораторной работе рассматривается методика получения временных и частотных характеристик на примере апериодического, которым представляется электрическая цепь, изображенная на рис. 2.5.
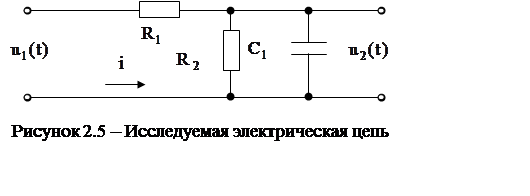 |
Составим уравнение динамики
электрической цепи представленной на рис. 2.5. Уравнение динамики системы
(звена) – уравнение, определяющее зависимость выходной величины системы (звена)
![]() от входной
от входной ![]() :
:
![]() . Оно может быть
записано в дифференциальной и операторной формах.
. Оно может быть
записано в дифференциальной и операторной формах.
Применительно к электрической цепи (рис. 2.5) имеем:
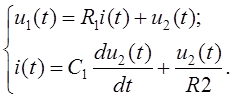
Исключая
промежуточную координату ![]() получим:
получим:
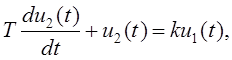 (2.12)
(2.12)
где: 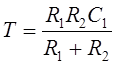 - постоянная времени;
- постоянная времени; 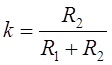 - коэффициент усиления звена.
- коэффициент усиления звена.
Переходя от дифференциальной формы записи уравнения (2.12) к операционной форме запишем:
![]() (2.13)
(2.13)
где: ![]() - изображения по Лапласу
функций времени
- изображения по Лапласу
функций времени ![]() .
.
Перейдем к передаточной функции
звена (системы) ![]() - функции, представляющей
собой отношение изображений по Лапласу выходной
- функции, представляющей
собой отношение изображений по Лапласу выходной ![]() и входной
и входной ![]() величин при нулевых начальных
условиях:
величин при нулевых начальных
условиях:
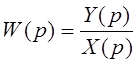 . (2.14)
. (2.14)
Передаточная функция рассматриваемой электрической цепи может быть определена из уравнения (2.13) в следующем виде:
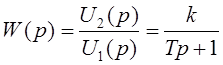 . (2.15)
. (2.15)
Звено с передаточной функцией (2.15) в теории автоматического управления получило название апериодического.
2.3 Методика выполнения работы
2.3.1 Использование Power System Blockset (имитационное моделирование)
Данная методика наиболее близка к лабораторным исследованиям реальных электрических цепей, что важно для изучения курса ТАУ электротехнических специальностей. В Power System Blockset модель объекта получается непосредственно из принципиальной схемы электрической цепи, воздействия формируются виртуальными источниками переменного или постоянного напряжения (тока), переходные процессы контролируются с помощью виртуальных контролирующих приборов (осциллограф, датчики токов и напряжений и т.п.).
Используя схему рис. 2.5,
создадим в Power System Blockset
следующую модель (рис. 2.6). Исследуемая цепь на рис. 2.6 представлена элементами
![]() (Parallel RLC Branch с параметрами:
(Parallel RLC Branch с параметрами: ![]() ) и
) и ![]() (Parallel RLC Branch с параметрами:
(Parallel RLC Branch с параметрами: ![]() ).
).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.