Методика снятия временных и частотных характеристик линейных динамических систем. Типовые воздействия, страница 5

- логарифмическая амплитудно-частотная характеристика (ЛАЧХ), вычисляемая как

                                                .                                       (4.7)

При построении  используется логарифмическая ось частот;

- логарифмическая фазо-частотная характеристика (ЛФЧХ) – ФЧХ, при построении которой используется логарифмическая ось частот.

ЛАЧХ и ЛФЧХ еще называют (в основном в зарубежной литературе) диаграммами Боде.

При анализе моделей часто оказываются полезными следующие параметры диаграмм Боде:

- частота среза (частота пересечения ЛАЧХ с осью абсцисс);

- запас по фазе             -      

- частота , при которой ЛФЧХ пересекает линию ;

- запас по амплитуде   -       .

4.3 Исходные данные

Для исследования динамических свойств типовых звеньев воспользуйтесь следующими выражениями передаточных функций:

1) для инерционного звена

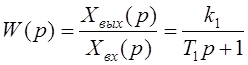                                          ;                              (4.8)

2) для колебательного звена

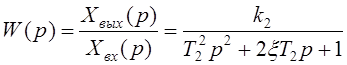                                  ;                      (4.9)

3) для инерционно-форсирующего звена

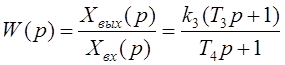                                       ;                         (4.10)

Базовые параметры звеньев (4.8) – (4.10) сведены в табл. 4.1.

Таблица 4.1 – Параметры исследуемых звеньев

Пара-метр	Номер варианта
	1	2	3	4	5	6	7	8	9	10
	1	2	10	5	4	40	1	20	20	100
	10	5	20	10	2	10	4	40	2	1
	50	100	1	40	50	2	100	5	50	40
, с	0.1	2	0.02	0.5	1	2	0.05	0.2	0.04	5
, с	0.01	0.02	0.1	0.2	0.5	0.05	0.04	0.4	0.25	0.02
, с	0.1	1	0.2	2	0.01	0.1	0.5	0.2	1	0.4
, с	1	0.1	2	0.2	0.1	0.01	0.1	1	0.2	0.01
	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5

4.4 Программа работы

4.4.1 Введите математическую модель апериодического звена в рабочую область системы MATLAB.

4.4.2 Получите графики частотных характеристик данного звена при базовых значениях параметров (см. табл. 4.1).

4.4.3 В имеющиеся графические окна (не удаляя полученные в пункте 4.4.2 графики) выведите также частотные характеристики этого же звена при коэффициенте уменьшенном и увеличенном в 10 раз. Сохраните графики в виде рисунков в файле отчета OTCH_LR3.DOC.

4.4.4 Сотрите информацию в графических окнах и снова повторите пункт 4.4.2. Наложите на полученные базовые графики частотные характеристики апериодического звена при уменьшенной и увеличенной в 2 раза постоянной времени. Сохраните графики в виде рисунков в файле отчета OTCH_LR3.DOC.

4.4.5 Аналогично пунктам 4.4.1 – 4.4.4 исследуйте влияние коэффициента усиления и постоянной времени на частотные свойства колебательного звена.

4.4.6 В дополнение к пункту 4.4.5 определите влияние коэффициента относительного затухания  на частотные характеристики звена второго порядка для следующего ряда значений .

4.4.7 Определите как повлияет перемена местами постоянных времени числителя и знаменателя передаточной функции инерционно-форсирующего звена на его частотные характеристики.

4.5 Содержание отчета

Отчет о лабораторной работе должен содержать:

1)  тему и цель работы;

2)  математическое описание типовых звеньев;

3)  рисунки, полученные согласно пунктов 4.4.1-4.4.7, с необходимыми подписями и пояснениями к ним;

4)  анализ влияния параметров типовых звеньев на их частотные характеристики.

4.6 Контрольные вопросы

4.6.1 Выведите уравнения амплитудно-фазовых характеристик исследуемых типовых звеньев.

4.6.2 Напишите выражения для фазо-частотных характеристик типовых звеньев.

4.6.3 Напишите выражения для амплитудно-частотных характеристик типовых звеньев.

4.6.4 Получите выражения ЛАЧХ исследуемых типовых звеньев.

4.6.5 Назовите достоинства частотных методов исследования.

4.6.6 Каким образом строятся асимптотические логарифмические частотные характеристики.

Список литературы

1. Теория автоматического управления / Под ред. А.В. Нетушила, - М.: Высш. шк., 1976. – 400 с.

2. Иващенко Н.Н. Автоматическое регулирование. – М.: Машиностроение, 1978. – 736 с.

3. Дьяконов В., Круглов В. MATLAB. Анализ, идентификация и моделирование систем. Специальный справочник. – СПб.: Питер, 2002. – 448 с.

5 ЛАБОРАТОРНАЯ РАБОТА №4

ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ СИСТЕМЫ ТРЕТЬЕГО ПОРЯДКА

5.1 Цель лабораторной работы

Целью данной лабораторной работы является исследование устойчивости системы третьего порядка с помощью различных методов – алгебраических и частотных.

5.2 Теоретическая подготовка

Необходимый материал для подготовки к лабораторной работе изложен в работах [1, c. 237-243, 149-163, 168-169], [2, c. 122-129, 100-104].

Для асимптотической устойчивости линейной системы необходимо, чтобы все корни характеристического уравнения лежали в левой полуплоскости корней. Характеристическое уравнение имеет вид:

,

где  - общий вид знаменателя передаточной функции замкнутой системы.

Примерный вид распределения корней устойчивой системы показан на рис. 5.1.

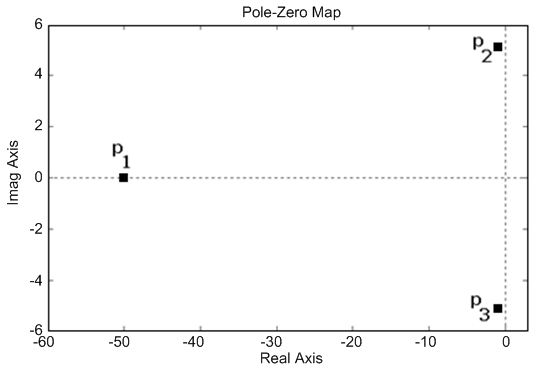
Рисунок 5.1 – Распределение корней

Как видно из рисунка, система имеет 3 корня p₁, p₂, p₃, причем все они расположены слева от мнимой оси. Наличие хотя бы одного корня в правой полуплоскости свидетельствует о том, что система является неустойчивой. Если один или несколько корней лежат непосредственно на мнимой оси, то система находится на границе устойчивости.

Данный метод проверки устойчивости при помощи распределения корней может быть использован только лишь для простых систем, не выше 3-4-го порядка. В системах более высокого порядка определение корней затруднено, т.к. нет общих выражений, связывающих значения корней с коэффициентами характеристического полинома D(p). Поэтому для сложных систем широкое распространение получили критерии устойчивости – некоторые правила, позволяющие судить об устойчивости, не прибегая к нахождению корней.