Методика снятия временных и частотных характеристик линейных динамических систем. Типовые воздействия, страница 6

Критерии устойчивости делятся на две группы: алгебраические (Рауса, Гурвица) и частотные (Найквиста, Михайлова). Изучите данные критерии, используя рекомендуемую литературу [1, 2].

В лабораторной работе проверка устойчивости системы выполняется двумя методами – с помощью распределения корней и с использованием критерия Найквиста. Критерий Найквиста имеет две разновидности: по амплитудно-фазовой характеристике (АФХ) разомкнутой системы, и по логарифмическим амплитудно-частотной (ЛАЧХ) и фазо-частотной (ЛФЧХ) характеристикам разомкнутой системы.

АФХ разомкнутой системы показана на рис. 5.2.

Согласно критерия Найквиста, САУ в замкнутом состоянии является устойчивой, если АФХ разомкнутой системы не охватывает точку [‑1, j0]. Точную формулировку критерия следует изучить, используя рекомендуемую литературу. Как видно из рис. 5.2, годограф не охватывает точку [-1, j0], значит, система в замкнутом состоянии устойчива.

Применение критерия Найквиста с использованием ЛАЧХ и ЛФЧХ позволяет не только установить факт устойчивости, но и легко получить запасы устойчивости по амплитуде и по фазе. Пример ЛАЧХ и ЛФЧХ разомкнутой системы показан на рис. 5.3.

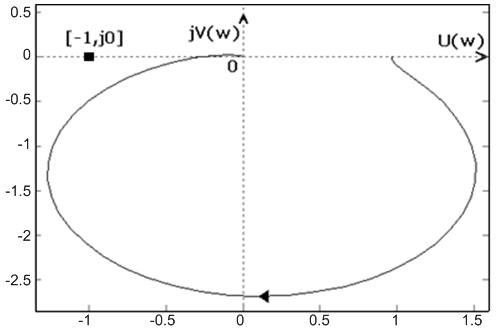
Рисунок 5.2 – АФХ разомкнутой системы

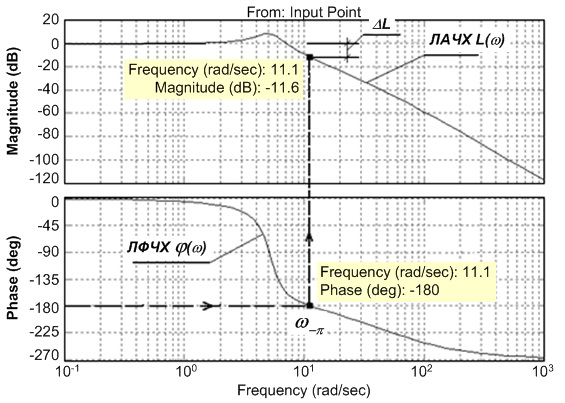
Рисунок 5.3 – ЛАЧХ и ЛФЧХ разомкнутой системы

Запас устойчивости по амплитуде может быть получен следующим образом:

-  найти частоту  - частоту, при которой фазовый сдвиг равен -180° (в рассматриваемом примере =11,1 рад/с);

-  найти амплитуду  - значение ЛАЧХ на частоте  (в рассматриваемом примере =-11,6 дБ);

-  определить запас устойчивости по амплитуде     .

В рассматриваемом примере на рис. 5.3 имеем  дБ. Поскольку запас устойчивости положительный, данная система является устойчивой. Если , система на границе устойчивости. При  система неустойчива.

5.3 Методика выполнения работы

В качестве объекта исследования принята система генератор-двигатель (Г-Д), управляемая при помощи безынерционного преобразователя и замкнутая отрицательной обратной связью по скорости двигателя. Структурная схема системы приведена на рис. 5.4.

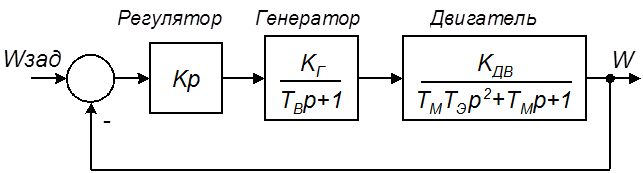
Рисунок 5.4 – Структурная схема исследуемой системы

Передаточная функция генератора:

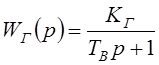                                                 ,                                         (5.1)

где   K_Г – коэффициент передачи генератора, T_В – электромагнитная постоянная времени обмотки возбуждения генератора.

Передаточная функция двигателя:

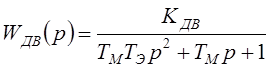                                        ,                               (5.2)

где   K_ДВ – коэффициент передачи двигателя, T_Э и T_М – соответственно электромагнитная и электромеханическая постоянная времени системы Г-Д. Для расчета параметров передаточной функции генератора и двигателя можно использовать следующие выражения:

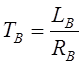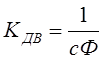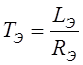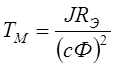                      ,     ,     ,    ,             (5.3)

где   L_В – индуктивность обмотки возбуждения генератора, R_В – сопротивление обмотки возбуждения генератора, с – конструктивная постоянная, Ф – поток двигателя, L_Э – индуктивность якорной цепи системы, R_Э – сопротивление якорной цепи, J – суммарный момент инерции, приведенный к якорю двигателя.

Как следует из структуры на рис. 5.4, исследуемая система регулирования скорости W является системой третьего порядка. Таким образом, в ней существует проблема устойчивости. При неверном расчете коэффициента передачи регулятора, или при отклонении параметров генератора или двигателя от расчетных значений запасы устойчивости системы могут уменьшиться или же система может потерять устойчивость.

Для исследования системы используем пакет Matlab/Simulink/Power System Blockset. Схема цифровой модели приведена на рис. 5.5.

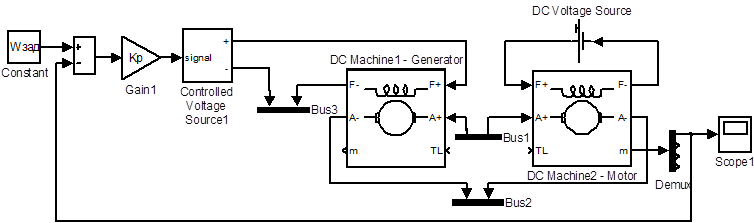
Рисунок 5.5 – Схема цифровой модели исследуемой системы

Моделирование как двигателя, так и генератора осуществляется с использованием блока «DC Machine». Для моделирования безынерционного управляемого источника питания обмотки возбуждения генератора применяется блок «Controlled Voltage Source». Описание параметров основных блоков цифровой модели приведено на рис. 5.6.

Для эмуляции вращения генератора с помощью некоторого приводного двигателя с постоянной скоростью W_Г =150 c^-1 следует ввести данное значение в качестве начальной скорости генератора (см. параметр “Initial speed”), а момент инерции генератора J_Г установить равным бесконечности. Это обеспечит постоянство скорости генератора независимо от его нагрузки.

«DC Machine1 – Generator»	«DC Machine1 – Motor»
а)	б)

Рисунок 5.6 – Параметры цифровой модели генератора (а) и двигателя (б)

Демультиплексор Demux обеспечивает перевод из Power System в Simulink следующих координат двигателя: скорость, ток якоря, ток возбуждения, вращающий момент. Поэтому обратную связь по скорости следует взять с 1-го выхода блока Demux.

Модель, собранная в соответствии с рис. 5.5, является существенно нелинейной вследствие особенностей внутренней реализации блоков «DC Machine». Для исследования устойчивости и снятия характеристик при помощи приложения LTI-Viewer следует перейти к линейной модели, показанной на рис. 5.7.

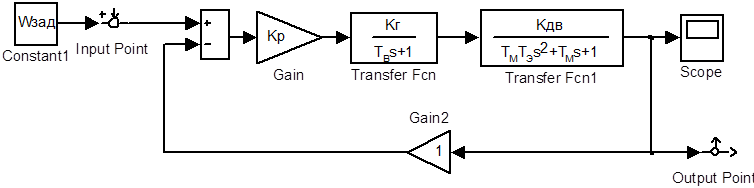
Рисунок 5.7 – Схема линеаризованной цифровой модели исследуемой системы

Поскольку якоря обеих машин включены последовательно, следует иметь ввиду, что суммарные значения сопротивления и индуктивности якорной цепи в 2 раза больше, чем у одной машины:

                                            ,   .                                    (5.4)

Блок Gain2 необходим для удобства при отключении/включении обратной связи по скорости. Если требуется отключить обратную связь, то следует задать коэффициент передачи блока Gain2 равным нулю.

5.4 Программа работы

5.4.1 Соберите цифровую модель согласно рис. 5.5. Исходные данные системы Г-Д приведены в табл. 5.1. Начальное значение коэффициента передачи регулятора K_Р возьмите равным K_Р=1. Получите переходный процесс скорости.

5.4.2 Варьируя коэффициент K_Р, подберите такие его значения, которые соответствуют следующему характеру переходного процесса скорости:

а) колебательный медленно затухающий (постоянные колебания, амплитуда которых со временем уменьшается – система устойчива);