1. Особенности условий работы и характеристики электрических цепей автоматики и связи. Электрическая цепь как модель.
Из курса ТОЭ электрическая цепь – совокупность взаимосвязанных устройств для передачи, распределения, преобразования электрической и других видов энергии и информации при условии, что проходящие в устройствах процессы можно описать с помощью ЭДС, тока и напряжения. Электрическая цепь, являющаяся элементом энергетических установок, в установившемся режиме работает при определенном напряжении постоянного или переменного тока с частотой 50Гц. В электрических цепях систем телемеханики и связи, образующих тракты передачи сигналов, изменяющиеся напряжения и токи являются случайными процессами. Рассм. простую цепь: уравнение равновесия напряжения имеет вид:
![]() или
или ![]()
Напряжение на выходе цепи:
![]() (1) - это частный случай ур-я
(1) - это частный случай ур-я ![]() , решение которого:
, решение которого:
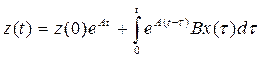 , где
, где ![]() – свободное движение из начального
состояния;
– свободное движение из начального
состояния; 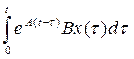 – вынужденное движение в результате
внешнего воздействия x(t). Решим ур-е (1) при нулевом начальном состоянии:
– вынужденное движение в результате
внешнего воздействия x(t). Решим ур-е (1) при нулевом начальном состоянии: ![]() или
или 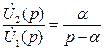 ,
, ![]()
Для выяснения условий передачи
от источника энергии к приемнику максимальной мощности, рассм. схему,
содержащую источник ЭДС с внутренним сопр-ем ![]() , к
зажимам которого подключен приемник с сопротивлением
, к
зажимам которого подключен приемник с сопротивлением ![]() .
Активная мощность приемника:
.
Активная мощность приемника: 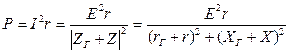
Мощность достигает наибольшего
значения при X=–XГ: 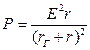 . Мощность максимальна при r=rГ.
. Мощность максимальна при r=rГ. 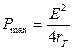
При X=–XГ мощность источника энергии 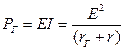 .
.
КПД: ![]() .
Т.о. есть 3 режима работы цепи: r < rГ – режим,
близкий к к.з.(КПД=0,5), r ≈ rГ – согласованный режим, r > rГ – режим,
близкий к х.х. (КПД→1). Особое место в современных системах автоматики и
телемеханики занимают рельсовые цепи (РЦ).
.
Т.о. есть 3 режима работы цепи: r < rГ – режим,
близкий к к.з.(КПД=0,5), r ≈ rГ – согласованный режим, r > rГ – режим,
близкий к х.х. (КПД→1). Особое место в современных системах автоматики и
телемеханики занимают рельсовые цепи (РЦ).
Элементы, способные поставлять энергию в цепь, наз-ют активными, элементы, накапливающие и расходующие энергию – пассивными. Эквивалентная схема цепи – модель реального объекта – является заменителем реальных объектов, который опирается на определенную теорию, выражающую компромисс между теорией и практикой и ориентирована на достижение определенной цели.
2. Канонические схемы 2хполюсников RC, свойства их сопротивлений и проводимостей.
2хполюсники разделяют по сложности на одно-, двухэлементные и т.д. и по хар-ру входящих в них элементов – на rC, LC, rL, rLC.
Схему 2хполюсника следует составлять так, чтобы можно было просто определить численные значения параметров ее элементов. Такое свойство присуще каноническим схемам.
Рассм. простейшую цепь с 2мя параметрами r и С:
Для данной цепи операторная проводимость
![]() . Параллельное подключение новых элементов не изменяет вида
. Параллельное подключение новых элементов не изменяет вида![]() .
.
Определим: 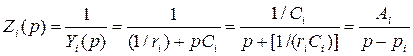 ,
,
Где![]() ;
; ![]()
Соединяя последовательно такие простейшие цепи, учитывая, что r может быть бесконечно большим, а С – бесконечно малым, получим каноническую схему:
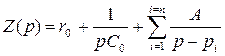 , где
, где![]() ;
; ![]() .
Каждому последовательному элементу соответствует одно из слагаемых в формуле.
Рассм. цепь:
.
Каждому последовательному элементу соответствует одно из слагаемых в формуле.
Рассм. цепь:
Для нее ![]() .
. 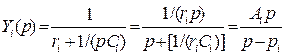
Для изменения свойств этой цепи новые элементы надо подключить параллельно – получим второй вид канонической схемы для 2хполюсников RC:
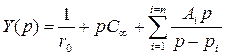 , где
, где![]() ;
; ![]()
для схемы:
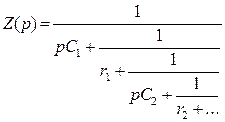
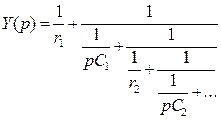
Это третья и четвертая канонические схемы 2хполюсника RC.
3. Канонические схемы 2хполбсников RL, свойства их сопротивлений и проводимостей.
2хполюсники разделяют по сложности на одно-, двухэлементные и т.д. и по хар-ру входящих в них элементов – на rC, LC, rL, rLC.
Схему 2хполюсника следует составлять так, чтобы можно было просто определить численные значения параметров ее элементов. Такое свойство присуще каноническим схемам.
Для данной цепи операторная проводимость
![]() .
.
Определим: 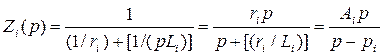 ,
,
Соединяя последовательно такие простейшие цепи получим каноническую схему:
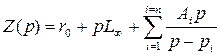 , где
, где![]() ;
; ![]() .
Каждому последовательному элементу соответствует одно из слагаемых в формуле.
Рассм. цепь:
.
Каждому последовательному элементу соответствует одно из слагаемых в формуле.
Рассм. цепь:
![]() .
.
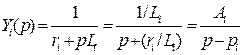
Для изменения свойств этой цепи новые элементы надо подключить параллельно – получим второй вид канонической схемы для 2хполюсников RC:
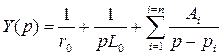 , где
, где![]() ;
; ![]()
4. Свойства функций входных сопротивлений и проводимостей пассивных 2хполюсников. Приемы построения 2хполюсных схем по заданным функциям Z(p) , Y(p).
Св-ва пассивной 2хполюсной цепи полностью определяются зав-тью ее вх. сопр-я или вх. проводимости от частоты ω (или параметра p). При синтезе цепи важно: какими могут (не могут) быть ф-ции Z(p) или Y(p). Если по этим ф-циям можно построить соответствующую эл. цепь, то их наз-ют физически реализуемыми. Входное сопр-е 2хполюсника в операторной форме:
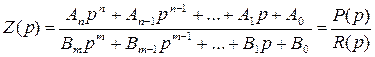
Реализуемая ф-ция сопротивления
(проводимости) должна иметь вид рациональной дроби. Сопр-е реальной цепи токам
высоких частот может иметь активный характер при n=m,
индуктивный характер и вид Lp, при n–m=1 и 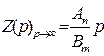 или емкостный характер
и вид 1/ (Сp), при n–m=–1и
или емкостный характер
и вид 1/ (Сp), при n–m=–1и 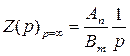 . Коэффициенты
. Коэффициенты ![]() и
и ![]() д. быть
вещ. и положи.. Многочлены в числителе и знаменателе рациональной дроби можно
представить в виде произведения множителей вида (p–pi), где pi – корни многочленов P(p) и Q(p):
д. быть
вещ. и положи.. Многочлены в числителе и знаменателе рациональной дроби можно
представить в виде произведения множителей вида (p–pi), где pi – корни многочленов P(p) и Q(p):
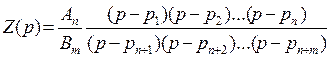
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.