Ответы на экзаменационные вопросы № 1-42 по дисциплине "Теория линейных электрических цепей железнодорожной автоматики, телемеханики и связи" (Электрическая цепь как модель. Импульсные характеристики и передаточные функции трансверсального и рекурсивного фильтров), страница 8

Значение t_{гр пр} на определенной частоте  хар-ет время запаздывания огибающей группы частотных составляющих сигнала, лежащих в узкой полосе частот вблизи ω₁. Для цепи с сосредоточенными параметрами

Для устранения ФЧ искажений используют корректоры группового времени прохождения. Фазовые хар-ки используемых в качестве корректоров 4хполюсников подбирают так, чтобы время прохождения в откорректированном тракте с включенным корректором  не зависело от частоты, т.е.

- фазовая хар-ка откорректированного тракта.

Мостовая схема с взаимообратными сопротивлениями:

; ;

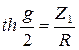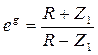
Независимость Z_М от частоты позволяет хорошо согласовать эти схемы с нагрузками. При реактивных сопр-ях Z₁ и Z₂:

;

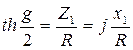
Значит ; ; ;

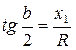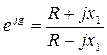
Отсюда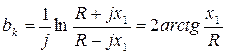

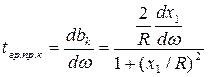
Фазовый контур 1ого порядка:

; ; ;

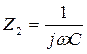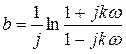
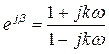. Отсюда , где k=L/R

Функция передачи: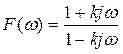

Фазовый контур 2ого порядка:

; ;

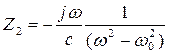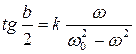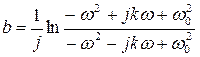
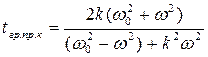
29. Цепи с распределенными параметрами. Первичные параметры электрической линии. Решение диф. ур-й линии для установившегося режима переменного тока.

При большой длине соединительных проводов, т.е. передаче эл. энергии по линии, длина кот. соизмерима с длиной волны эл/магн. Колебания, нельзя не учитывать сопр-е, индуктивность и емкость, распределенные по всей ее длине. Эл. и магн. Поля в этом случае распределены вдоль линии и пространственно совмещены. Такая линия – эл. цепь с распределенными параметрами.

Для получения исходных соотношений, определяющих процессы в цепях с сосредоточенными параметрами, используют первичные параметры: сопр-е проводов R (Ом/км), их индуктивность L (Гн/км), проводимость изоляции G (1/Ом·км), емкость проводов С (Ф/км).

 

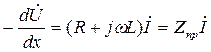
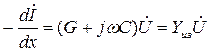
Это диф. ур-я линии.

Продиф-ем 1ое Ур-е по х:

   => 

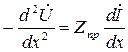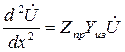
Обозначим , тогда:

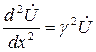, γ – коэффициент распространения волны

Отсюда

Соответственно для тока:

 =>

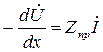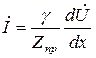
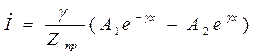
Причем 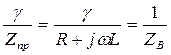, где Z_B – волновое сопр-е линии.

Решение системы диф. ур-й:

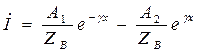
Где

Величины γ и Z_B – вторичные параметры линии.

30. Анализ решения диф. ур-й линии. Волновые процессы в линии (падающие и отраженные волны напряжения и тока в линии, волновые параметры линии).

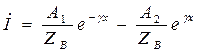
Пусть x=0, тогда , где А₁ и А₂ – составляющие напряжения. Будем писать вместо А₁ и А₂ и .

Рассм. 1ое слагаемое ур-я  .

Полагая, что  получим

На комплексной плоскости это выр-е изображают вращающим вектором с нач. фазой – βх. Это выр-е математически представляет собой волну, движущуюся от начала линии к ее концу – падающую.

Рассм. 2ое слагаемое:

- мгнов. Значения

Это ур-е соответствует волне, движущейся от конца линии к ее началу – отраженной.

Напряжение в каждой точке линии равно сумме падающей и отраженной волн:

А ток:

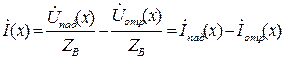
Волновое сопр-е определяет отношение напряжения к току в отдельной волне (падающей или отраженной) в любой точке однородной линии.

Величины γ и Z_B – вторичные (волновые) параметры линии.

31. Взаимодействие падающих и отраженных волн в линии. Коэффициент отражения.

Напряжение в каждой точке линии равно сумме падающей и отраженной волн:

А ток:

Коэффициент отражения – отношение напряжения отраженной волны к напряжению падающей волны:

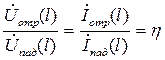
Для численного определения коэф-та отраж-я рассм. усл-я равнове-сия напряжений и токов в конце линии.     

;

;

Отсюда

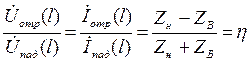
Рассм. 3 случая:

1. х.х.: , то η=+1

2. к.з.: , то η=–1

3. нагрузка согласована, т.е. , то η=0.

32. Связи между напряжениями и токами на входе и выходе линии (общий случай).

Связь между напряжениями и токами на входе и выходе линии характеризует передающие св-ва последней и позволяет определить напряжение и ток на входе линии, кот. обеспечивают на ее выходе напряжение и ток, необх. для работы приемника.  

Отсюда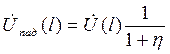

Получим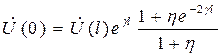

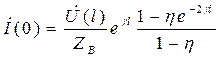
Усл-е передатчика хар-ет вх. сопр-е:

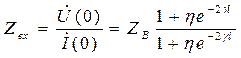
Напряжение и ток в произвольной точке линии, находящейся на расст. x от ее начала и  от ее конца:

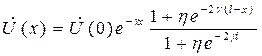
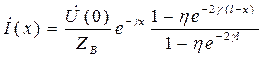
33. Особенности волновых процессов в согласованной и электрически длинной линии. Связи между напряжениями и токами на входе и выходе линии.