Ответы на экзаменационные вопросы № 1-42 по дисциплине "Теория линейных электрических цепей железнодорожной автоматики, телемеханики и связи" (Электрическая цепь как модель. Импульсные характеристики и передаточные функции трансверсального и рекурсивного фильтров), страница 4

Теорию 4хполюсника используют для создания электрических цепей с определенными передающими свойствами, которые задают в виде частотных зависимостей параметров, связывающих напряжение и токи, а по параметрам выбирают схему замещения, по которой строят синтезирующую цепь.

10. Схема замещения 4хполюсника Т, ее матрицы параметров Z и ABCD.

Составим для данной схемы ур-я 4хполюсников:

;   

Рассмотрим в отдельности режимы х.х. и к.з.

При х.х. (зажимы 3 и 4 разомкнуты):

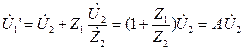
Ток в сопротивлениях Z₁ и Z₂ одинаковый, значит

При к.з. (3 и 4 замкнуты накоротко):

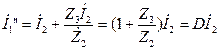
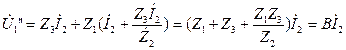
Полные напряжения и ток на входе:

;   

Это и есть ур-е схемы замещения Т.

Между коэффициентами A, B, C, D вып-ся соотношение AD-BC=1. 

Ур-я схемы Т так же можно представить в виде:

Отсюда найдем: ;

Матрица параметров ABCD:

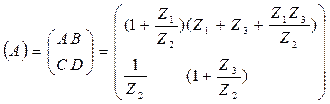
Матрица параметров Z – матрица сопротивлений х.х.:

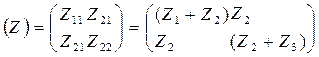
11. Схема замещения 4хполюсника П, ее матрицы параметров Y и ABCD.

Рассмотрим режимы х.х. и к.з. При х.х. напряжение на входе равно сумме напряжения U₂ и падения напряжения на Z₁.

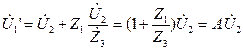
Ток на входе равен сумме токов в сопротивлениях Z₂ и Z₃.

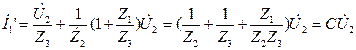
При к.з. ;

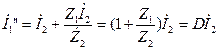
Полные напряжение и ток на входе:

;   

Матрица параметров ABCD:

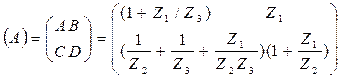
Между коэффициентами A, B, C, D вып-ся соотношение AD-BC=1. 

Ур-я схемы П также можно представить в виде:

Матрица параметров Y – матрица проводимостей к.з.:

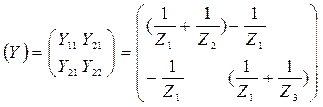
12. Симметричные схемы замещения Т и П и их параметры передачи.

Каждую из схем можно представить, как составленную из 2х частей, называемых схемами Г:

Для схемы Г:

Отсюда

   

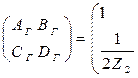
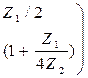
Ур-я симметричных схем для схемы Т:

Ур-я симметричных схем для схемы П:

Матрицы параметров ABCD для  схемы Т:

   

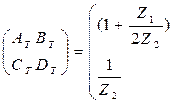
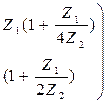
Матрицы параметров ABCD для  схемы П:

   

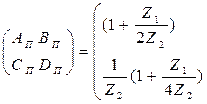
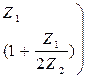
Для всякого симметричного 4хполюсника A=D. При этом для обратимых 4холюсников

13. Последовательное и параллельное соединение 4хполюсников. Определение параметров соединения.

Последовательное соединение характеризуется соотношением:

; ;

; .

Для 2х соединенных 4хполюсников:

;

;

;

;

Отсюда:

Значит ; ;

; .

Запишем матрицу сопротивлений:

 = + 

Т.о. каждый последовательно соединяемый 4хполюсник следует характеризовать матрицей сопротивлений х.х. и эти матрицы сложить. Число соединяемых 4хполюсников м.б. любым.

Параллельное соединение:

Параллельное соединение характеризуется соотношением:

; ;

; .

Для 2х 4хполюсников:

Отсюда:

;

Отсюда:

 = + 

Т.о. матрица проводимостей параллельно соединенных 4хполюсников равна сумме матриц проводимостей4хполюсников, входящих в соединение.

14. Цепочечное соединение 4хполюсников. Определение параметров соединения.

При цепочечном соединении 2х 4хполюсников:

; ; ;

; ; .

Тогда для определения параметров соединения воспользуемся уравнениями передачи:

;

;

Отсюда получим:

Группируя члены этих уравнений и убирая штрихи, получим:

Полученные ур-я ввязывают напряжение и ток на входе с напряжением и током на выходе.

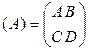Если 4хполюсники, входящие в цепочечное соединение характеризовать матрицей , то все соединение можно охарактеризовать матрицей:

   

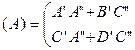
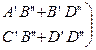
Матрица (А) цепочечного соединения 4хполюсников – произведение матриц  и  4хполюсников, входящих в это соединение.

  

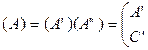
15. Цепочечное соединение 4хполюсников при согласованных на-грузках. Собственные параметры передачи 4хполюсников Z_x и g.

Рассм. каким д.б. сопр-е приемника Z_н одного 4хполюсника, чтобы оно совпадало с вх. сопр-ем Z_вх.

Найдем Z_н=Z_х, при котором Z_вх=Z_н =Z_х:

             

Пусть 4хполюсник симметричен и A=D:и

Сопр-е Z_х – характеристическое сопр-е 4хполюсника определяет отношение напряжения к току на его входе и выходе при нагрузке на сопр-е Z_х. Нагрузка 4хполюсника на приемник наз-ся согласованной. При согласованной нагрузке:

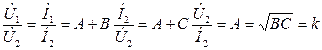
k – коэффициент передачи. 

Часто для характеристики свойств 4хполюсника пользуются величиной:

При согласованном цепочечном соединении 4хполюсников их логарифмические характеристики g складываются.