Электротехника \ Теория линейных электрических цепей железнодорожной автоматики, телемеханики и связи

Ответы на экзаменационные вопросы № 1-42 по дисциплине "Теория линейных электрических цепей железнодорожной автоматики, телемеханики и связи" (Электрическая цепь как модель. Импульсные характеристики и передаточные функции трансверсального и рекурсивного фильтров), страница 3

Эти связи можно представить по-разному в зависимости от того, какие 2е из величин заданы. Ур-я с параметрами Z: Пусть заданы токи I₁, I₂, надо найти U₁, U₂. Если схема разветвленной цепи, рассматриваемой как 4хполюсник, известна, для нее можно составить с-му ур-й узловых напряжений: ; .

Δ – определитель матрицы проводимости к.з. цепи

Δ₁₁ и Δ₁₂ – его алгебраические дополнения.

Коэффициенты при токах – сопротивления, поэтому:

; .

Z₁₁ – вх. сопр. 4хполюсника, измеренное со стороны входа 1 при разомкнутом входе 2; Z₂₂ – вх. сопр. 4хполюсника, измеренное со стороны входа 2 при разомкнутом входе 1; Z₁₂, Z₂₁ – сопр. передачи, измеренные при размыкании обоих входов.

Данные ур-я наз-ют уравнениями 4хполюсника. Все вместе сопр-я Z_ij – сопротивления (параметры) холостого хода 4хполюсника.

Представленная 4хполюсником цепь, содержащая только пассивные элементы, обладает свойством обратимости. В этом случае Z₁₂=Z₂₁, а 4хполюсник называют обратимым (взаимным).

Схему двухконтурной цепи, соответствующую ур-ям обратимого 4хполюсника, называют схемой замещения Т-обратимого 4хполюсника.

Она содержит три сопр-я, кот.

однозначно определяются 3мя независимыми параметрами

4хполюсника.

4хполюсних называют симметричным, если равны его вх. сопр-я Z₁₁=Z₂₂. У симметричного обратимого 4хполюсника независимы только 2 параметра, остальные определяются из Z₁₂=Z₂₁ и Z₁₁=Z₂₂. Схема замещения 4хполюсника:

Ур-я 4хполюсника в матричной форме:

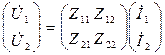или

Матрицу (Z) называют матрицей сопротивлений х.х. 4хполюсника.

8. Ур-я 4хполюсника с Y-параметрами. Физ. смысл параметров. Связь между параметрами в случаях симметричности и обратимости. Схемы замещения.

Ур-я 4хполюсника ; можно решить относительно токов I₁ и I₂:

;

Обозначим, , , . Тогда:

; (1), где Y₁₁ – вх. проводимость 4хполюсника, измеренная на входе при закороченном выходе; Y₂₂ – вх. проводимость, измеренная на выходе при закороченном входе; Y₁₂, Y₂₁ – проводимость передачи, измеренная при закороченных входах.

Для обратимого 4хполюсника Y₁₂=Y₂₁. Схема замещения П-обратимого 4хполюсника:

У обратимого симметричного 4хполюсниканезависимы 2 параметра: входная проводимость и проводимость передачи, остальные определяем из уравнений: Y₁₂=Y₂₁ и Y₁₁=Y₂₂. Варианты 2хузловых схем, соответствующих ур-ям (1), с зависимыми источниками тока:

Уравнения (1) в матричной форме:

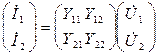или

Матрицу (Y) называют матрицей проводимостей короткого замыкания 4хполюсника.

9. Уравнения 4хполюсника с параметрами ABCD. Физ. смысл параметров. Связь между параметрами в случаях симметричности и обратимости. Примеры применения 4хполюсных цепей в устройствах АТ и связи.

Пусть рассматриваемая 4хполюсная цепь представляет собой промежуточное звено в какой-то системе передачи эл. энергии и имеет вход (зажимы 1) и выход (зажимы 2).

В данном случае наиболее удобны ур-я 4хполюсника, решенные относительно U₁ и I₁.

;

Принято обозначать: , , ,.

Тогда: ;

Где - величина, обратная коэффициенту трансформации по напряжению при разомкнутых зажимах 2; – величина, обратная Y₂₁ – проводимости передачи при замкнутых зажимах 2; – величина, обратная Z₂₁ – сопротивлению передачи при разомкнутых зажимах 2 ; - величина, обратная, коэф-ту трансформации по току при закороченных зажимах 2.