40. Принципы построения активных RC-фильтров. Примеры реализации.
1. RC фильтры с развязывающими усилителями: на выходе фильтра rC включают усилитель с большим вх. сопр-ем. Если фильтрующие св-ва недостаточны, цепочечно соединяем несколько одинаковых фильтров с усилителями на выходах. Ф-ция передачи соединения:
, где F1 – ф-ция передачи простейшего пассивного фильтра; k –
коэф-т усиления усилителя; n –
число входящих в цепочку звеньев.
2. RC фильтры
на операционных усилителях с частотно-зависимой обратной связью. Ф-ция передачи соединения с ОС: 
, где k1 – коэф-т
усиления усилителя; k2 – ф-ция передачи цепи ОС. Ф-ция передачи этого
фильтра: 
, где 
В более сложных случаях цепь
ОС считаем 4хполюсником, кот. хар-ся ф-цией передачи: 
3. фильтры на ОУ с многопетлевой ОС. Малочувствительны к изменению параметров эл-тов. На схеме Y – пассивная цепь rC и 3мя внеш. узлами, характеризуемыми матрицей проводимостей к.з.
Вследствие большого вх. сопр-я
усилителя с усилением k 
В то же время 
. Т.о.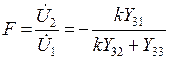 
4. фильтры, содержащие частотно-зависимые отрицательные сопр-я
Для реализации ЧЗОС следует в
схеме принять 
; 
тогда
; 
; 
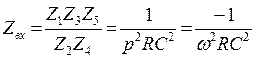На вещественных частотах он имеет отриц. активное сопр-е. Параметры ЧЗОС не зав. от усиления входящих в его схему усилителей.
5. настраиваемые фильтры на интеграторах.
Ф-ция 2ого порядка м.б. реализована содержащими интеграторы каноническими схемами:
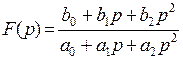
Во всех случаях а0=1. При b1=b2=0, b0=H ф-ция представляет собой ф-цию передачи ФНЧ, при b0=b1=0, b2=H –ФВЧ, b0=b2=0, b1=H – ПФ.
41. Цифровые фильтры (элементная база, виды реализации). Линейная модель цифрового фильтра. Рекурсивные и трансверсальные цифровые фильтры.
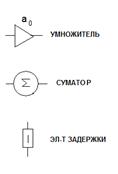
ЦФ – устройства, осуществляющие линейную фильтрацию сигналов цифровыми методами (т.е. исп-е ср-в цифровой вычислительной техники). Цифровую фильтрацию сигналов осуществляют на основе операций только 3х типов: задержки, сложения и умножения. ЦФ м.б. реализован 2мя способами: 1. программный способ реализации эффективен при моделировании различных систем цифровой обработки сигналов, т.к. позволяет легко изменять алгоритм фильтрации; 2. аппаратный способ реализации основан на использовании цифровых интегральных схем, представляющих собой регистры сдвига, сумматоры и др.
Реакция цепи на единичный импульс – импульсная хар-ка G(t). Если реакция фильтра на единичный импульс представлена конечным числом отсчетов, то G(kT) сост. из конечного числа членов K. В этом случае реакция фильтра имеет конечное число отсчетов при К=3:
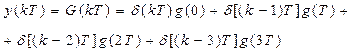
Этому выр-ю соотв. схема, кот. вх. последовательность отсчетов x(kT) преобр-ет в вых. y(kT) и представляет собой дискретный фильтр с импульсной хар-кой G(kT). Эта схема – линейная модель ЦФ:
Данный фильтр не имеет ОС и явл-ся нерекурсивным ЦФ. У рекурсивного ЦФ есть цепь ОС. Его схема:
42. Импульсные хар-ки и передаточные ф-ции трансверсального и рекурсивного фильтров.
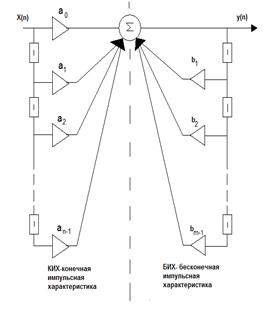
Реакцию цепи на единичный импульс называют импульсной характеристикой цепи. Если единичный импульс подать на вход цифрового фильтра, то сигнал на его выходе будет представлять собой дискретную последовательность значений, следующих с интервалом Т называемым интервалом дискретизации. Этот сигнал является импульсной характеристикой цифрового фильтра. Если реакция фильтра на единичный импульс представлена конечным числом отсчетов, фильтр не имеет цепей обратной связи и называется нерекурсивным. Если импульсная характеристика содержит бесконечное число отсчетов, то фильтр имеет цепь обратной связи и он представляет собой так называемый рекурсивный фильтр. В технической литературе, посвященной цифровым и дискретным фильтрам, использована и другая терминология: фильтры с конечной импульсной характеристикой (КИХ-фильтры) и с бесконечной импульсной характеристикой (БИХ-фильтры). Любой реальный нерекурсивный фильтр является и КИХ-фильтром. Рекурсивные фильтры, как правило, есть БИХ-фильтры.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.