Вычисления
по формулам (59), (60) производим для ряда значений ![]() .
Результаты сводим в табл.6.
.
Результаты сводим в табл.6.
Таблица 6
|
мм |
Н×мм/мм |
мм |
|
0 100 200 300 400 500 |
2230 2020 1400 370 -1080 -2940 |
-6,34 -5,88 -4,60 -2,81 -1,04 0 |
Угловое перемещение крайних сечений цилиндрической оболочки и пластинки
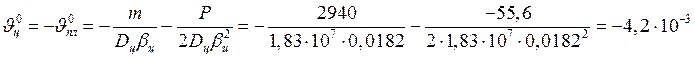 рад.
рад.
По результатам расчета строим графики радиальных изгибающих моментов в пластинке и меридиональных изгибающих моментов в цилиндрической оболочке, (рис.19), а также графики прогибов пластинки и радиальных перемещений точек цилиндрической оболочки, (рис.20).
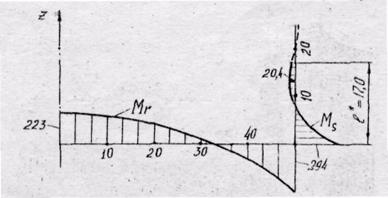
Рис.19. Изгибающие моменты в элементах сосуда
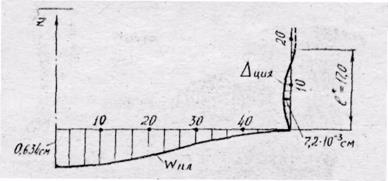
Рис.20. Перемещения элементов сосуда
3.3. Оценка прочности сосуда
Наиболее
опасным является крайнее сечение ![]() цилиндрической
оболочки. Внутренние усилия в этом сечении:
цилиндрической
оболочки. Внутренние усилия в этом сечении:
-
меридиональный изгибающий момент ![]() Н×мм/мм;
Н×мм/мм;
-
кольцевой изгибающий момент ![]() Н×мм/мм;
Н×мм/мм;
-
нормальное меридиональное усилие 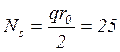 Н/мм;
Н/мм;
-
нормальное кольцевое усилие ![]()
Напряжения в рассматриваемом сечении:
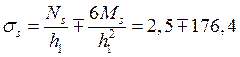 МПа,
(61)
МПа,
(61)
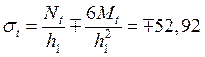 МПа. (62)
МПа. (62)
Верхние знаки в формулах (61), (62) относятся к наружной поверхности оболочки, нижние – к внутренней. Распределение напряжений по толщине оболочки показано на рис.21.
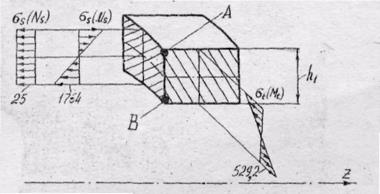
Рис.21. Напряжения в крайнем сечении
цилиндрической оболочки.
Меридиональные напряжения:
– на
наружной поверхности оболочки, (точка А), ![]() МПа,
МПа,
– на
внутренней поверхности, (точка В), ![]() МПа;
МПа;
Кольцевые напряжения:
– на
наружной поверхности оболочки ![]() МПа,
МПа,
– на
внутренней поверхности ![]() МПа.
МПа.
Радиальные
напряжения ![]() по второй гипотезе Кирхгофа-Лява равны
нулю.
по второй гипотезе Кирхгофа-Лява равны
нулю.
Таким
образом, эквивалентные напряжения по III
теории прочности в точках ![]() и
и ![]() составляют:
составляют:
![]() МПа,
МПа,
![]() МПа.
МПа.
Условие прочности при расчете по допускаемым напряжениям.
![]() МПа
МПа ![]() .
.
Величина
допускаемого напряжения ![]() задается при расчете
сосуда.
задается при расчете
сосуда.
Интересно
сопоставить величины напряжений в днищах различной формы при одной и той же
нагрузке. Очевидно, что величина напряжений в днище определяется величиной
краевого изгибающего момента. Расчет показывает, что при нагружении сосуда, рассмотренного
в п.2, газовым давлением ![]() МПа в точках
сопряжения сферической и цилиндрической оболочек возникает краевой изгибающий
момент
МПа в точках
сопряжения сферической и цилиндрической оболочек возникает краевой изгибающий
момент ![]() Н×мм/мм,
величина же краевого момента в точках сопряжения цилиндрической оболочки с
коническим днищем
Н×мм/мм,
величина же краевого момента в точках сопряжения цилиндрической оболочки с
коническим днищем ![]() Н×мм/мм. Таким
образом, с прочностной точки зрения оптимальным в нашей задаче является днище
сферической формы, за ним следует коническое днище, величина напряжений в
котором примерно в 1,5 раза больше. Самой неудачной оказывается конструкция
сосуда с плоским днищем, напряжения в котором по величине в 15 раз превышают
напряжения в сферическом днище. Конструкцию сферического днища можно
усовершенствовать, положив
Н×мм/мм. Таким
образом, с прочностной точки зрения оптимальным в нашей задаче является днище
сферической формы, за ним следует коническое днище, величина напряжений в
котором примерно в 1,5 раза больше. Самой неудачной оказывается конструкция
сосуда с плоским днищем, напряжения в котором по величине в 15 раз превышают
напряжения в сферическом днище. Конструкцию сферического днища можно
усовершенствовать, положив ![]() ,
, ![]() . В этом случае, как показывает расчет,
величины краевого момента
. В этом случае, как показывает расчет,
величины краевого момента ![]() и усилия
и усилия ![]() оказываются близкими к нулю, и в сосуде
реализуется практически безмоментное напряженное состояние, являющееся
наиболее выгодным вследствие равномерности работы материала оболочки. Величина
напряжений снижается при этом более, чем в 2 раза.
оказываются близкими к нулю, и в сосуде
реализуется практически безмоментное напряженное состояние, являющееся
наиболее выгодным вследствие равномерности работы материала оболочки. Величина
напряжений снижается при этом более, чем в 2 раза.
Необходимо отметить, что при проектировании приходится учитывать также ряд иных факторов: конкретные условия работы конструкции, наличие оборудования для ее изготовления, технологичность конструкции, стоимость изготовления и т.д. Поэтому в отдельных случаях оптимальными могут оказаться коническое или даже плоское днище, наиболее простое в изготовлении. Для обеспечения прочности сосуда осуществляют различные конструктивные мероприятия: увеличивают толщину стенки сосуда, усиливают места сопряжений посредством отбортовки днищ и.т.п.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.