 , Н×мм
/мм. (18)
, Н×мм
/мм. (18)
Нормальное кольцевое усилие
![]()
![]() Н/мм.
(19)
Н/мм.
(19)
Радиальное перемещение
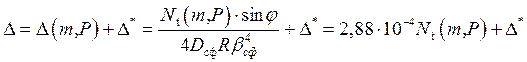 , мм. (20)
, мм. (20)
Координаты границы зоны краевого эффекта
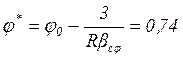 ,
(21)
,
(21)
![]() мм.
(22)
мм.
(22)
Расчет
по формулам (18), (19), (20) выполняем для ряда значений аргумента ![]() . Значения безмоментных составляющих
нормального кольцевого усилия
. Значения безмоментных составляющих
нормального кольцевого усилия ![]() и радиального перемещения
и радиального перемещения
![]() заимствуем из безмоментного решения,
выполненного в 1 части работы. Значения функций,
заимствуем из безмоментного решения,
выполненного в 1 части работы. Значения функций, ![]() ,
, ![]() ,
принимаем по табл. 2 Приложения. Результаты расчета сводим в табл.2.
,
принимаем по табл. 2 Приложения. Результаты расчета сводим в табл.2.
Таблица 2
Результаты расчета сферической оболочки
|
|
рад |
Н×мм/мм |
Н/мм |
Н/мм |
Н/мм |
мм |
мм |
мм |
|
0 |
1,05 |
194,0 |
-53,3 |
30,2 |
-23,1 |
-13,25 |
5,35 |
-7,9 |
|
0,4 |
1,01 |
77,6 |
-49,6 |
30,1 |
-19,5 |
-12,1 |
5,2 |
-6,9 |
|
0,8 |
0,97 |
8,8 |
-37,3 |
30,0 |
-7,3 |
-8,9 |
5,1 |
3,8 |
|
1,2 |
0,92 |
-24,0 |
-22,9 |
29,9 |
+7,0 |
-5,3 |
4,9 |
-0,4 |
|
1,6 |
0,88 |
-33,6 |
-12,6 |
29,8 |
17,2 |
-2,8 |
4,7 |
+1,9 |
|
2,0 |
0,84 |
-30,7 |
-4,9 |
29,7 |
24,8 |
-1,1 |
4,5 |
3,4 |
|
2,4 |
0,80 |
-22,8 |
-0,4 |
29,6 |
29,2 |
-0,1 |
4,3 |
4,2 |
|
2,8 |
0,76 |
-14,4 |
+1,7 |
29,5 |
31,2 |
+0,3 |
4,2 |
4,5 |
|
3,2 |
0,72 |
-7,5 |
2,3 |
29,4 |
31,7 |
0,4 |
4,0 |
4,4 |
Угловые перемещения крайних сечений оболочек:
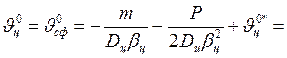
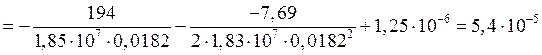 рад.
рад.
По результатам расчета строим графики распределения меридиональных изгибающих моментов нормальных кольцевых усилий и радиальных перемещений вдоль образующей сосуда в области сопряжения цилиндрической и сферической оболочек (рис.8, 9, 10). На графиках видно, что изгиб оболочек локализован в узких зонах, примыкающих к крайним сечениям. За пределами этих зон напряженно-деформированное состояние оболочек практически не отличается от безмоментного состояния.
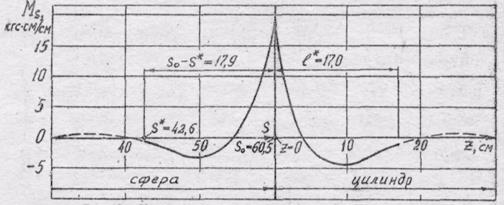
Рис.8. Меридиональный изгибающий момент в зоне сопряжения цилиндрической и сферической оболочек
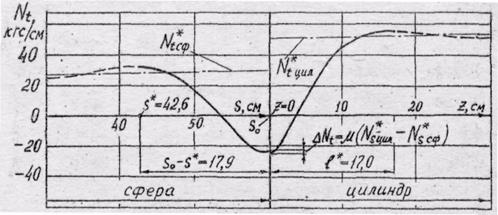
Рис.9. Нормальное кольцевое усилие в зоне сопряжения цилиндрической и сферической оболочек
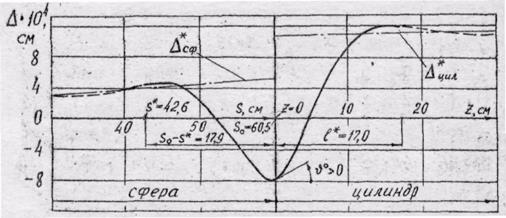
Рис. 10. Радиальные перемещения в зоне сопряжения цилиндрической и сферической оболочек
2.2. Расчет узла сопряжения цилиндрической и конической оболочек
Как и в предыдущем случае, для решения задачи применяем метод сил. Расчетная схема представлена на рис.11.
Осевое
усилие ![]() , приложенное к краю конической оболочки,
разложено на две составляющие: меридиональное усилие
, приложенное к краю конической оболочки,
разложено на две составляющие: меридиональное усилие ![]() и
радиальное усилие
и
радиальное усилие ![]() . Усилие
. Усилие ![]() и
давление
и
давление ![]() среды на коническую оболочку образуют
самоуравновешенную систему, от воздействия которой в оболочке возникает
безмоментное напряженное состояние. Изгиб оболочки вызывают краевая моментная
нагрузка
среды на коническую оболочку образуют
самоуравновешенную систему, от воздействия которой в оболочке возникает
безмоментное напряженное состояние. Изгиб оболочки вызывают краевая моментная
нагрузка ![]() и радиальное усилие
и радиальное усилие ![]() .
.
Безмоментное
напряженное состояние в цилиндрической оболочке возникает от воздействия
осевого усилия ![]() и давления
и давления ![]() . Изгиб оболочки вызывают краевой момент
. Изгиб оболочки вызывают краевой момент ![]() и усилие
и усилие ![]() .
.
Осевое
усилие ![]() находим из условия равновесия конической
оболочки:
находим из условия равновесия конической
оболочки:
![]() , (23)
, (23)
где ![]() определяется формулой (35) в 1 части
работы. Принимая во внимание, что
определяется формулой (35) в 1 части
работы. Принимая во внимание, что ![]() , получим:
, получим:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.