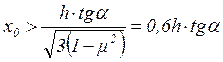Информатика и выч. техника \ Методы и алгоритмы расчетов на прочность в САПР

Расчет тонкостенных конструкций оболочечного типа. Часть 2: Методические указания (Расчет тонкостенных оболочек вращения по моментной теории. Расчет сосуда с плоским днищем), страница 2


   при   ,                                            (3)


и приемлема 10%-ная погрешность расчета.

Рис.5.  Расчетная схема замкнутой в вершине конической оболочки

При допустимой 5%-ной погрешности расчета условие (3) заменяют следующим:


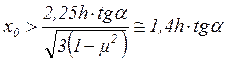   при   .                                          (4)


Одновременно не следует упускать из виду проверку условия тонкостенности оболочки. Так как для конической оболочки , то условие тонкостенности принимает вид:

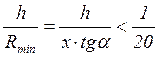
или

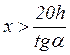                                                                     (5)


Отсюда, в частности, вытекает, что окрестность вершины конической оболочки 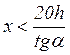  не удовлетворяет условию тонкостенности и должна быть исключена из рассмотрения.

Внутренние усилия и перемещения в зоне краевого эффекта, примыкающей к краю оболочки , определяются по формулам, приведенным в Приложении для края оболочки . На рис.5 указаны положительные направления радиального , осевого  и углового  перемещений.

1.3. Сферическая оболочка

Формулы для расчета длинной сферической оболочки, незамкнутой в вершине, даны в Приложении.

Замкнутая в вершине  сферическая оболочка, (рис.6), при допустимой 10%-ной  погрешности  расчета считается длинной, если выполняется условие


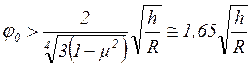   при                                     (6)


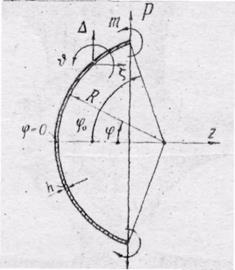
Рис.6. Расчетная схема сферической оболочки,

 замкнутой в вершине

Если допустимая погрешность  расчета составляет 5%,  то условие  (6) необходимо  заменить  следующим:


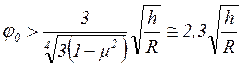   при   .                                           (7)


Внутренние  усилия и перемещения в зоне  краевого  эффекта, примыкающей к краю оболочки, определяют по формулам, приведенным в  Приложении для края  сферической оболочки . На рис.6 указаны, положительные направления радиального , осевого  и углового  перемещений.

Рассмотрим применение  моментной  теории  на примере расчета сосуда,  состоящего из оболочек различной геометрической формы.

2. ПРИМЕР РАСЧЕТА СОСУДА  ПО МОМЕНТНОЙ ТЕОРИИ

Рассмотрим сосуд, расчет которого по безмоментной теории был выполнен в 1 части настоящей работы. Методами моментной теории оболочек проведем исследование напряженно-деформированного состояния элементов сосуда в зонах краевого эффекта, примыкающих к  точкам сопряжения цилиндрической оболочки со  сферической крышкой и коническим днищем. Сохраним при этом численные значения геометрических и физических параметров сосуда, а также  параметров нагрузки.

2.1.  Расчет узла сопряжения цилиндрической и сферической оболочек

Для решения задачи применяем метод сил. Разделяем оболочки и заменяем воздействие их друг на друга осевым усилием , кгс/см, радиальной сосредоточенной  нагрузкой  Н/мм и моментной  нагрузкой  Н•мм/мм,    приложенными к краям оболочек, как показано на рис.7.

Осевое усилие , приложенное к краю сферической оболочки, целесообразно разложить на две составляющие:  усилие , направленное по касательной к меридиану оболочки, и радиальное усилие .

Усилие , и давление , действующие на сферическую оболочку, образуют самоуравновешенную систему, вызывающую в оболочке безмоментное напряженное состояние. Краевая моментная нагрузка  и радиальное усилие  вызывают изгиб сферической оболочки.

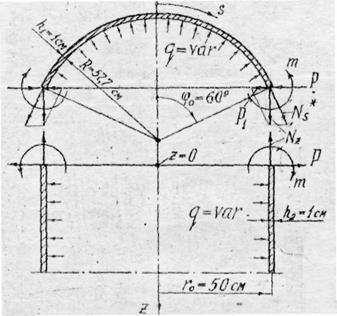
Рис.7. Расчетная схема узла сопряжения

цилиндрической и сферической оболочек

В цилиндрической оболочке безмоментное напряженное состояние возникает от осевого усилия  и давления .  Изгиб оболочки вызывают радиальное усилие  и момент .

Осевое усилие  находим из условия равновесия сферической оболочки, проектируя на ось  действующие на нее усилия:


                                                                  (8)


Осевая равнодействующая  сил давления среды на сферическую крышку сосуда определяется формулой (33) в 1 части работы. Принимая во внимание, что  получим:


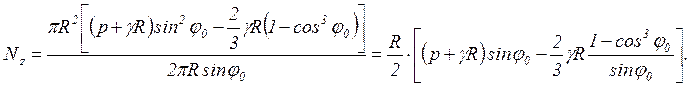             (9)


Подставляя численные данные,  находим:  Н/мм.

Для контроля правильности полученного результата можно воспользоваться соотношением , где  - меридиональное напряжение в цилиндрической оболочке, полученное по безмоментной теории.

Далее  находим усилия  и :

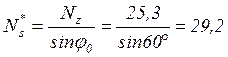 Н/мм,

  Н/мм.

Краевое усилие  и  момент  определяем из условия совместной работы элементов сосуда (цилиндрической и сферической оболочек),  полагая равными нулю относительные радиальное и угловое перемещения их крайних сечений: 

Скачать файл