Информатика и выч. техника \ Методы и алгоритмы расчетов на прочность в САПР

Расчет тонкостенных конструкций оболочечного типа. Часть 2: Методические указания (Расчет тонкостенных оболочек вращения по моментной теории. Расчет сосуда с плоским днищем), страница 7

Меридиональные напряжения:

- на наружной поверхности оболочки (точка А):

  МПа;

- на внутренней поверхности  (точка В):

   МПа.

Кольцевые  напряжения:

- на наружной поверхности оболочки (точка А):

 МПа;

- на внутренней поверхности  (точка В):

  МПа.

Нормальные напряжения в площадках, параллельных срединной поверхности оболочки, по второй гипотезе Кирхгофа-Лява равны нулю. Схемы напряженного состояния в рассматриваемых точках представлены на рис.16.

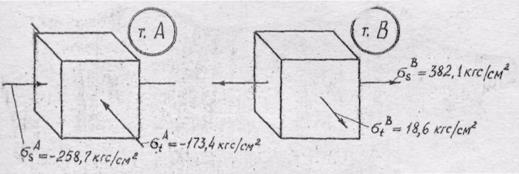
Рис.16.  Схемы напряженного состояния

в точках наружной и внутренней поверхности

крайнего сечения конической оболочки

Эквивалентные  напряжения определяем по III теории прочности:

 МПа,

   МПа.

Условие  прочности при расчете  по допускаемым напряжениям:

  МПа , где  – допускаемое напряжение, величина которого задается при проектировании сосуда.

Отметим, что безмоментная теория дает иной результат. Так в краевом сечении конической оболочки  МПа,  МПа, (см. 1 часть работы). Следовательно,  МПа, что более чем в 3 раза отличается от истинного значения. Таким образом, расчет по моментной теории не только позволяет определить действительное напряженно-деформированное состояние сосуда, но и существенно меняет оценку его прочности по сравнению с безмоментным решением.

3.   РАСЧЕТ СОСУДА С ПЛОСКИМ ДНИЩЕМ

Рассмотрим цилиндрический сосуд с плоскими крышкой и днищем, нагруженный внутренним газовым давлением , (рис.17).

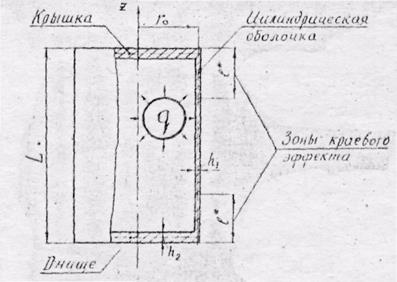
Рис.17. Схема сосуда с плоским днищем

Геометрические размеры , , ,  и механические характеристики материала сосуда  и  известны. Полагаем, что длина сосуда удовлетворяет условию:

.

Расчет участка цилиндрической оболочки вне зон краевого эффекта производим по безмоментной теории. Из уравнения Лапласа определяем кольцевое напряжение:

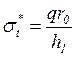;                                                                         (38)


из уравнения равновесия сосуда – меридиональное напряжение:

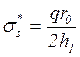;                                                                         (39)


после чего находим радиальное и угловое перемещения:

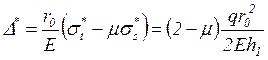,                                              (40)


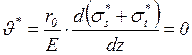.                                                       (41)


Для расчета узла сопряжения цилиндрической оболочки с плоским днищем применяем метод сил. Днище рассматриваем как тонкую круглую пластинку. Разделяем рассматриваемый узел на составные элементы и заменяем их воздействие друг на друга краевыми усилиями ,  и краевой моментной нагрузкой . Расчетная схема представлена на рис. 18.

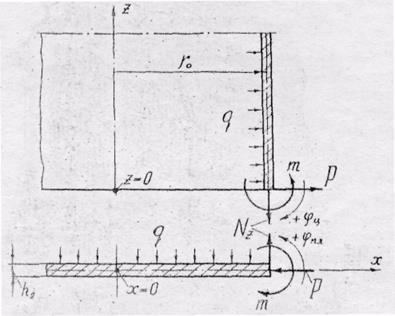
Рис.18. Расчетная схема узла сопряжения

цилиндрической оболочки с пластинкой

На рисунке показаны положительные направления углов поворота цилиндрической оболочки и пластинки.

Осевое усилие  определяем из условия равновесия пластинки:


,                                                               (42)


откуда

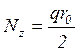   Н/мм.                                                                 (43)


Краевое усилие  и момент  находим из условия совместной работы цилиндрической оболочки и пластинки, полагая равными радиальные и угловые перемещения их крайних сечений:

,                                                                            (44)


.                                                                           (45)


Знак минус в соотношении (45) объясняется тем, что положительные направления углов поворота пластинки и цилиндрической оболочки не совпадают (см. рис.18).

Соотношение  (44) можно упростить, полагая, что пластинка нерастяжима в своей плоскости:

.                                                                        (46)


Погрешность, вводимая в расчет этим допущением, пренебрежимо мала.

Выражения для перемещений крайнего сечения цилиндрической оболочки получаем по принципу суперпозиции, используя формулы Приложения, а также выражения (40) и (41):


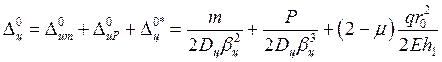,                              (47)


Скачать файл