,
. (10)
Условия (10) можно переписать в следующем виде:
,
. (11)
где 
, 
, 
, 
-
абсолютные радиальные и угловые перемещения крайних сечений рассматриваемых
оболочек.
Воспользовавшись принципом независимости действия сил, из условий (II) получаем следующие соотношения:
,
, (12)
где
индексами 
и 
обозначены
перемещения крайних сечений цилиндрической и сферической оболочек
соответственно от краевых радиальных усилий и краевого момента, значком 
помечены перемещения от безмоментных
составляющих нагрузки, т.е. от 
и 
- для сферической оболочки; от 
и - для цилиндрической
оболочки.
Нетрудно убедиться, что рассматриваемые оболочки являются длинными, их параметры удовлетворяют условиям (2) и (7). Поэтому для их расчета мы можем воспользоваться формулами, приведенными в приложении к настоящей разработке.
Подставляя
в соотношения (12) выражения для перемещений крайних сечений оболочек из
Приложения, получаем систему линейных алгебраических уравнений относительно
неизвестных
и :
,
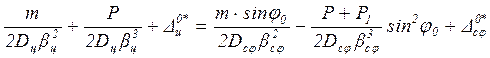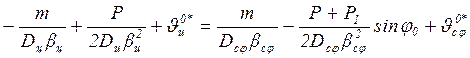, (13)
где
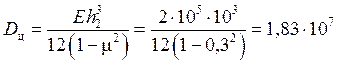Н×мм,
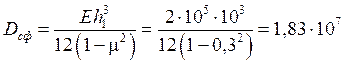Н×мм,,
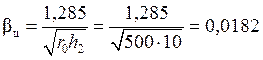1/мм,
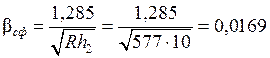1/мм ,
Значения безмоментных составляющих перемещений заимствуем из результатов расчета сосуда по безмоментной теории в 1 части разработки:
, 
,
, 
.
Подставляем численные значения коэффициентов в систему (13) и находим ее решение:
m = 194 Н×мм /мм,
P = –7,69 Н/мм.
Определяем теперь внутренние усилия и перемещения в элементах рассматриваемого узла по формулам Приложения.
2.1.1. Расчет цилиндрической оболочки
Меридиональный изгибающий момент
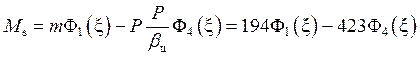, Н×мм
/мм. (14)
Нормальное кольцевое усилие
Н/мм.
(15)
Радиальное перемещение
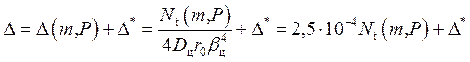, мм. (16)
Длина зоны краевого эффекта
мм.
Вычисления по формулам (14), (15), (16) выполняем для ряда
значений аргумента 
в интервале 
с шагом 
.
Значения функций 
, 
,
принимаем по табл.2 Приложения. Значения безмоментных
составляющих нормального кольцевого усилия 
и
радиального перемещения 
заимствуем из решения
задачи по безмоментной теории в 1 части работы. Результата расчета сводим в
табл.1.
Таблица 1
|
|
мм |
Н×мм/мм |
Н/мм |
Н/мм |
Н/мм |
мм |
мм |
мм |
|
0 |
0 |
194 |
-75,7 |
51,4 |
-24,3 |
-18,9 |
11,0 |
-7,9 |
|
0,4 |
22 |
59,9 |
-63,4 |
51,6 |
-11,8 |
-15,9 |
11,0 |
-4,9 |
|
0,8 |
44 |
-13,1 |
-44,3 |
51,7 |
+ 7,4 |
-11,1 |
11,0 |
-0,1 |
|
1,2 |
66 |
-43,1 |
-25,2 |
51,8 |
26,6 |
- 6,3 |
11,0 |
+4,7 |
|
1,6 |
88 |
-47,4 |
-12,5 |
51,9 |
39,4 |
-3,1 |
11,1 |
8,0 |
|
2,0, |
110 |
-39,1 |
- 3,6 |
52,0 |
48,4 |
- 0,9 |
11,1 |
10,2 |
|
2,4 |
132 |
-27,0 |
+ 1,1 |
52,1 |
53,2 |
+ 0,3 |
11,1 |
11,4 |
|
2,8 |
154 |
-15,8 |
3,0 |
52,2 |
55,2 |
0,8 |
11,2 |
12,0 |
|
3,2 |
176 |
-7,3 |
3,2 |
52,3 |
55,5 |
0,8 |
11,2 |
12,0 |
2.1.2. Расчет сферической оболочки
Меридиональный изгибающий момент
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
,
,
,
,
,
,