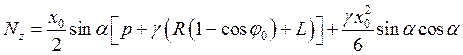Расчет тонкостенных конструкций оболочечного типа. Часть 2: Методические указания (Расчет тонкостенных оболочек вращения по моментной теории. Расчет сосуда с плоским днищем), страница 5

 = 43,6  Н/мм.            (24)

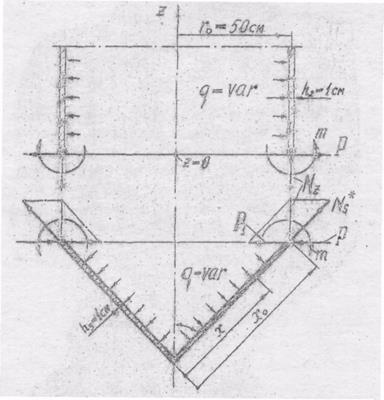
Рис. 11. Расчетная схема узла сопряжения

цилиндрической и конической оболочек

Далее

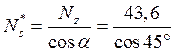 = 61,7  Н/мм,

 = 43,6 Н/мм.

Для контроля полученных результатов можно воспользоваться соотношениями:

,

, где ,  - меридиональные напряжения в крайних сечениях цилиндрической и конической оболочек, вычисленные по безмоментной теории.

Краевое усилие  и момент  определяем из условия совместной работы цилиндрической и конической оболочек, полагая равными нулю относительные радиальное и угловое смещения их крайних сечений:

,

.                                                                   (25)

Условия (25) можно записать в следующем виде:

,

,                                                                  (26)

где , , ,   – абсолютные радиальные и угловые перемещения крайних сечений рассматриваемых оболочек.

Воспользовавшись принципом независимости действия сил, из условий (26) получаем соотношения:

,

,                                      (27)

где индексами  и  обозначены перемещения крайних сечений цилиндрической и конической оболочек соответственно от краевого усилия и краевого момента;  значком * помечены перемещения, вызванные безмоментными составляющими нагрузки.

В рассматриваемой задаче цилиндрическая и коническая оболочки являются длинными, так как их параметры удовлетворяют условиям (2) и (4). Поэтому для расчета применимы формулы Приложения.

Подставляя в соотношения (27) выражения для перемещений крайних сечений оболочек, получим систему линейных алгебраических уравнений относительно неизвестных  и :

,

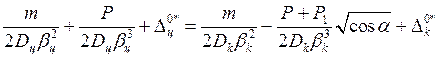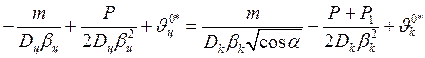,                               (28)

где

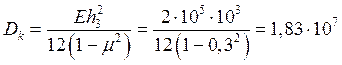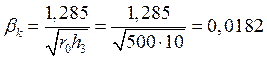  Н×мм,

   1/мм.

Параметры  и  вычислены ранее (см. стр. 11).

Значения безмоментных составляющих перемещений заимствуем из результатов расчета сосуда по безмоментной теории. При этом знаки величин угловых перемещений изменяем на обратные, учитывая изменение направления оси оболочки , (см. рис.10 в 1 части работы и рис.11 настоящей работы):

  мм,    ,

 мм,    .

Подставляем численные значения коэффициентов в систему (28) и находим ее решение:

 Н×мм/мм,

 Н/мм.

Затем по формулам Приложения определяем внутренние усилия и перемещения в элементах рассматриваемого узла.

2.2.1.  Расчет цилиндрической оболочки

Меридиональный изгибающий момент

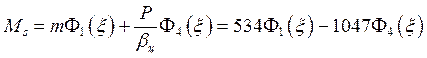,  Н×мм/мм.                (29)

Нормальное кольцевое усилие

  Н/мм.                                                (30)

Радиальное перемещение

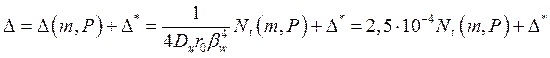  мм.            (31)