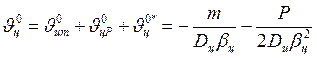 .
(48)
.
(48)
Для расчета пластинки воспользуемся методом начальных параметров. Общие уравнения изгиба круглой пластинки в нашем случае имеют следующий вид:
- радиальный изгибающий момент
![]() , (49)
, (49)
- угол поворота нормали к пластинке
![]() , (50)
, (50)
- прогиб пластинки
![]() , (51)
, (51)
где 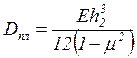 - цилиндрическая жесткость пластинки;
- цилиндрическая жесткость пластинки; ![]() ,
, ![]() -
начальные параметры, (радиальный изгибающий момент и прогиб в центре пластинки);
-
начальные параметры, (радиальный изгибающий момент и прогиб в центре пластинки);
![]() ,
, ![]() ,
, ![]() ,
, ![]() –сопровождающие
функции.
–сопровождающие
функции.
Начальные
параметры определяем из граничных условий: при ![]() :
: ![]() ,.
,.
![]() .
.
Подставляя граничные условия в соответствующие уравнения изгиба пластинки, получаем следующие соотношения:
![]()
![]() ,
,
![]() ,
(52)
,
(52)
из
которых выражаем ![]() и
и ![]() через
краевой момент
через
краевой момент ![]() :
:
![]() ,
(53)
,
(53)
![]() . (54)
. (54)
Находим
угол поворота наружного контура пластинки ![]() ,
подставляя выражение (53) для
,
подставляя выражение (53) для ![]() в уравнение (50):
в уравнение (50):
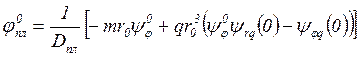 (55)
(55)
Подставляя
в соотношения (45), (46) выражения (47), (48), (55) для перемещений крайних
сечений оболочки и пластинки, получаем систему линейных алгебраических
уравнений относительно неизвестных ![]() и
и ![]() :
:
![]()
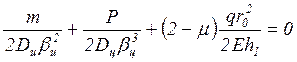 ,
,
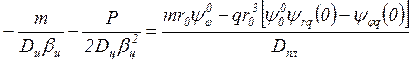 . (56)
. (56)
Решая
систему, находим ![]() и
и ![]() , затем
производим расчет элементов сосуда, определяя внутренние усилия и перемещения.
, затем
производим расчет элементов сосуда, определяя внутренние усилия и перемещения.
Для численного расчета примем следующие данные:
r0 = 500 мм, E = 2×105 МПа,
L = 3000 мм, m = 0,3,
h1 = h2 = 10 мм, q = 0,1 МПа
В этом случае
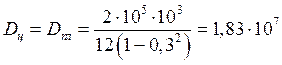 Н×мм,
Н×мм,
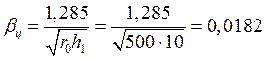 1/мм,
1/мм,
![]() мм.
мм.
Значения
сопровождающих функций при ![]() :
:
![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
Подставляем численные значения коэффициентов в систему (56) и находим ее решение:
![]() Н×мм/мм,
Н×мм/мм,
![]() Н/мм, после чего выполняем расчет
элементов сосуда.
Н/мм, после чего выполняем расчет
элементов сосуда.
3.1. Расчет цилиндрической оболочки
Меридиональный изгибающий момент
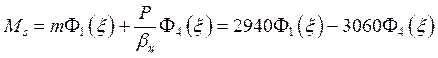 Н×мм/мм.
(57)
Н×мм/мм.
(57)
Радиальное перемещение
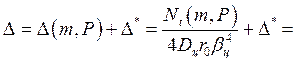
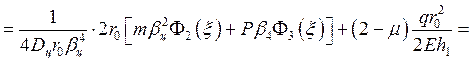
![]() мм. (58)
мм. (58)
Результаты
расчета по формулам (57) и (58) для ряда значений аргумента ![]() сводим в табл.5.
сводим в табл.5.
|
|
мм |
Н×мм/мм |
мм |
мм |
мм |
|
0 |
0 |
294 |
-0,01 |
0,01 |
0 |
|
0,4 |
2,2 |
178 |
-0,07 |
0,01 |
-0,06 |
|
0,8 |
4,4 |
88 |
-0,82 |
0,01 |
-0,072 |
|
1,2 |
6,6 |
29 |
-0,07 |
0,01 |
-0,06 |
|
1,6 |
8,8 |
-4,5 |
-0,049 |
0,01 |
-0,039 |
|
2,0 |
11,0 |
-18,0 |
-0,029 |
0,01 |
-0,019 |
|
2,4 |
13,2 |
-20,4 |
-0,14 |
0,01 |
-0,004 |
|
2,8 |
15,4 |
-18,2 |
-0,004 |
0,01 |
+0,006 |
|
3,2 |
17,8 |
-12,0 |
-0,001 |
0,01 |
0,011 |
3.2. Расчет плоского днища
По формулам (53) и (54) находим значения начальных параметров:
![]() Н×мм/мм,
Н×мм/мм,
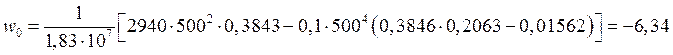 мм.
мм.
Подставляя значения
![]() и
и ![]() в
выражения (49) и (51), получаем расчетные формулы для радиального изгибающего
момента и прогиба пластинки:
в
выражения (49) и (51), получаем расчетные формулы для радиального изгибающего
момента и прогиба пластинки:
![]() , (59)
, (59)
![]() . (60)
. (60)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.