Пусть теперь нужно построить сглаживающий сплайн в
произвольной области, которая не может рассматриваться как один интервал
сглаживания. Разобьем исходную область несколько подинтервалов: ![]() . На каждом подинтервале используются
отдельные базисные функции, отличные от нуля только на этом отрезке. Далее
поступаем так: для каждой i-ой точки определяем
какому интервалу (включая границы) она принадлежит, вычисляем локальную матрицу
(5.3), используя базисные функции, соответствующие найденному интервалу,
заносим локальную матрицу в соответствующую позицию глобальной матрицы
(соответствие определяется по принадлежности точки интервалу). Глобальная
матрица будет симметричной и имеет ленточную структуру, ширина ленты равна
четырем, решаем методом Холецкого.
. На каждом подинтервале используются
отдельные базисные функции, отличные от нуля только на этом отрезке. Далее
поступаем так: для каждой i-ой точки определяем
какому интервалу (включая границы) она принадлежит, вычисляем локальную матрицу
(5.3), используя базисные функции, соответствующие найденному интервалу,
заносим локальную матрицу в соответствующую позицию глобальной матрицы
(соответствие определяется по принадлежности точки интервалу). Глобальная
матрица будет симметричной и имеет ленточную структуру, ширина ленты равна
четырем, решаем методом Холецкого.
Как уже отмечалось выше, функция ![]() очень быстро убывает на ранних временах и
достаточно медленно на поздних, то есть имеет сильно меняющуюся производную.
Это плохо сказывается на качестве сглаживающего сплайна, поэтому целесообразно
перейти в логарифмические координаты, в которых
очень быстро убывает на ранних временах и
достаточно медленно на поздних, то есть имеет сильно меняющуюся производную.
Это плохо сказывается на качестве сглаживающего сплайна, поэтому целесообразно
перейти в логарифмические координаты, в которых ![]() изменяется
уже достаточно плавно, и провести сглаживание в новых координатах. После того,
как построили сплайн делается обратный переход. Так как в нашем случае и время,
и ЭДС - неотрицательные величины, то для перехода в логарифмическую шкалу, достаточно
сделать преобразования
изменяется
уже достаточно плавно, и провести сглаживание в новых координатах. После того,
как построили сплайн делается обратный переход. Так как в нашем случае и время,
и ЭДС - неотрицательные величины, то для перехода в логарифмическую шкалу, достаточно
сделать преобразования ![]() . Если среди
. Если среди ![]() или
или ![]() имеются
нулевые значения, то вместо нулей берутся некоторое малые числа
имеются
нулевые значения, то вместо нулей берутся некоторое малые числа ![]() и
и ![]() ,
которые в нашем случае можно выбрать например так:
,
которые в нашем случае можно выбрать например так:
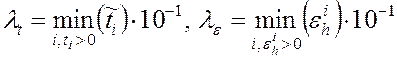 .
.
При таком выборе исключается
ситуация, когда два различных значения исходной кривой отобразятся в одно
значение новой кривой. Обратный переход делается аналогично, только вместо
логарифмирования выполняем потенцирование (естественно с учетом того, что ![]() и
и ![]() должны
снова стать нулями).
должны
снова стать нулями).
Посмотрим, на практические результаты восстановления ЭДС для импульса-ступеньки с использованием регуляризации.
Исходная ЭДС — ЭДС для полусинуса, вычисленная в пакете TELMA и зашумленная (шум 5%, высокочастотный), разрешено возрастание на 5%, в подинтервалы сглаживания включаются точки, в которых значения ЭДС отличаются не более, чем на порядок.
Рис.5.2 Относительные отклонения ЭДС для импульса-ступеньки, восстановленной из зашумленной ЭДС от восстановленной из незашумленной
Ошибка все еще значительно больше уровня шума, однако теперь это хотя бы можно назвать результатом (раньше и этого не имели, см. рис.4.9), который можно использовать для предварительного восстановления параметров горизонтально-слоистой среды. Отметим, что хотя сглаженная кривая и имеет в некоторых точках большую ошибку, все равно предпочтительнее использовать гладкую кривую, так как для нее лучше работает процедура подбора горизонтально-слоистой модели, кроме того, в других случаях сглаженная кривая может иметь меньшую ошибку (см. рис.5.3).
Исходная ЭДС получена суммированием для полусинуса и зашумлена (шум 5%, высокочастотный), разрешено возрастание на 5%, в подинтервалы сглаживания включаются точки, в которых значения ЭДС отличаются не более, чем на порядок.
Рис.5.3 Относительные отклонения восстановленной ЭДС от истинной
На следующем рисунке показан результат восстановления с регуляризацией, когда возрастание запрещено, и когда разрешено. Входные данные из предыдущего теста.
Рис.5.4 Результат регуляризации когда возрастание запрещено, и когда разрешено (показан фрагмент)
В заключении рассмотрим еще одну модификацию процедуры регуляризации. Допустим в результате описанных выше способов была восстановлена некоторая ЭДС для импульса-ступеньки, используем ее для подбора характеристик горизонтально-слоистой среды в программном комплексе HORIZON. После подбора в нашем распоряжении будет кривая ЭДС, соответствующая подобранной среде. Используем ее при регуляризации введя вместо добавки (5.1) добавку
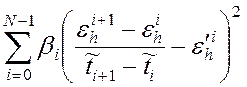 , где
, где ![]() -
значение производной, вычисленное по кривой, полученной после подбора среды.
Выполнив действия, аналогичные приведенным для первой регуляризации, можно
легко получить добавку в правую часть системы (5.2), сама система при этом не
изменится.
-
значение производной, вычисленное по кривой, полученной после подбора среды.
Выполнив действия, аналогичные приведенным для первой регуляризации, можно
легко получить добавку в правую часть системы (5.2), сама система при этом не
изменится.
![]() ,
,
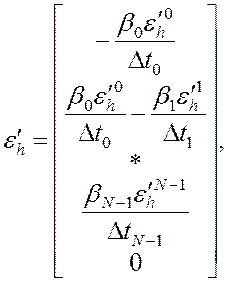
![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.