Разложение импульса.Разложение ЭДС.Использование регуляризации, страница 5

Теперь матрица имеет строго верхнетреугольный вид, причем на диагонали стоят ненулевые элементы. Первые N штук (от 0-го до N-1-го) отличны от нуля потому, что коэффициент  и слагаемое  - обязательно входит в i-е уравнение, по построению сетки. Последний диагональный элемент имеет вид , учитывая, что  из (2.3) , получаем, что для равенства нулю последнего элемента, нужно чтобы , то есть , а это не выполняется для построенной сетки. Из выше сказанного можно заключить, что матрица СЛАУ не вырожденна.

Так как матрица оказалась верхнетреугольной, то нет необходимости сначала собирать ее всю, а потом решать систему, можно это делать параллельно: начиная с последнего, получить очередное уравнение, решить его, сохранить результат и перейти к следующему. При таком подходе можно сэкономить память (будет храниться только одно уравнение, вместо всей матрицы), численные затраты останутся такими же. Однако далее нам придется вводить регуляризирующие добавки при решении СЛАУ и в этом случае будет выгодней собрать всю матрицу целиком, правда лишь для временного использования.

3.2.2.  Аппроксимация ЭДС сплайном

Перейдем к аппроксимации функции  кубическим сплайном. Введем шаблонные кусочно-кубические базисные функции на единичном отрезке (см. рис.3.2) [9].

Рис.3.2 Шаблонные кусочно-кубические базисные функции

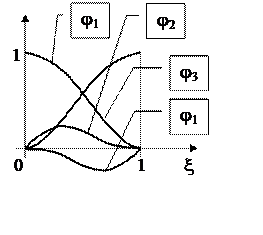Функция  равна единице при  и нулю при  и имеет нулевые производные при  и , функция  имеет производную  и  и нулевые значения при  и , функция  равна нулю при  и единице при  и имеет нулевые производные при  и , а функция  имеет производную  и  и нулевые значения при  и . Коэффициенты  каждого из таких кубических полиномов  могут быть легко получены по их значениям и значениям их производных на концах шаблонного единичного отрезка. Так для коэффициентов функции  получаем систему

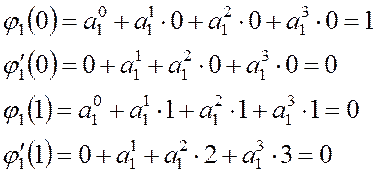                   (3.12)

Аналогичные системы могут быть получены и для коэффициентов остальных трех кубических полиномов, причем матрицы у всех этих систем одинаковые и совпадают с матрицей системы (3.12). Поэтому все четыре системы для коэффициентов  четырех кубических полиномов  можно объединить в одно матричное уравнение

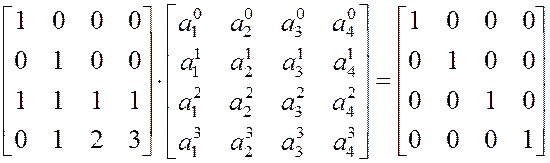
Из этого уравнения сразу следует, что матрица коэффициентов  функций  может быть вычислена как обратная матрица системы (3.12):

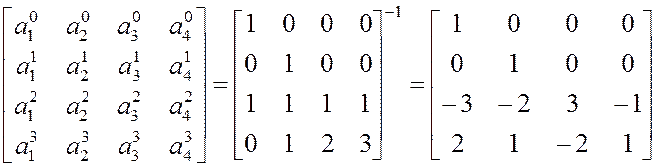
то есть

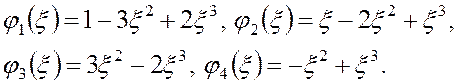
Кусочно-кубические функции для произвольного интервала , в локальной нумерации имеющего вид  можно получить из шаблонных путем замены переменной:

.

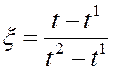Отметим, что для получения локальных базисных функций  и  из шаблонных  и , недостаточно просто заменить переменную  на , для того, чтобы производная в узлах равнялась единице базисные функции должны иметь вид

.

Действительно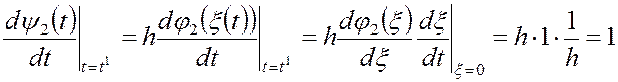

На отрезке  будем представлять функцию  в виде линейной комбинации локальных базисных функций , причем коэффициентами этой линейной комбинации являются значения функции и  значения ее производной в узлах:

,  (3.13)

где .

Значения производной в узлах, получим используя квадратичную интерполяцию. Допустим, что сплайн строится на интервале . Получим значение производной в точке , для этого на интервале  построим интерполяционный полином Лагранжа [3,10], продифференцируем  его и найдем значение производной в точке . Опять введем локальную нумерацию узлов:

.

 

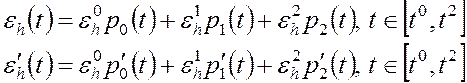
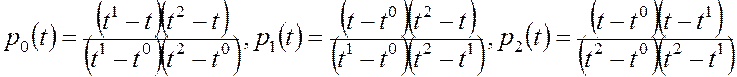
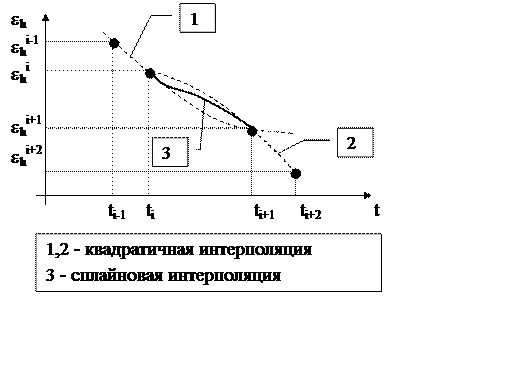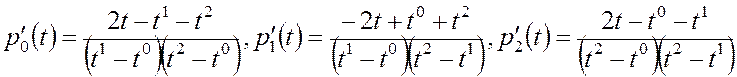
Рис.3.4 Построение сплайна

Аналогично находится производная в точке :

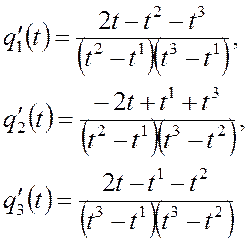
Подставим все это в (3.13) и перегруппируем относительно :

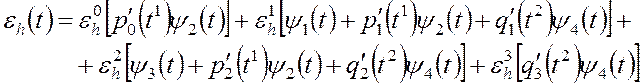
Для интервалов  и  также используется квадратичная интерполяция, только производную вычисляем не в среднем узле, а в крайнем.

При сплайновой аппроксимации у матрицы СЛАУ будет заполнен верхний треугольник и еще одна диагональ, лежащая снизу от главной. Решать такую систему можно либо методом LU-разложения [3,10], адаптированным под структуру матрицы, либо методом Гаусса, исключая дополнительную диагональ. Метод Гаусса в данном случае будет иметь немного меньшие вычислительные затраты.

4.  Анализ результатов