Остается вопрос выбора коэффициентов регуляризации ![]() , причем брать все одинаковые нельзя, так
как
, причем брать все одинаковые нельзя, так
как ![]() изменяется в большом диапазоне значений
(например, от 10-6 до 10-18). К сожалению, априорно
выбрать
изменяется в большом диапазоне значений
(например, от 10-6 до 10-18). К сожалению, априорно
выбрать ![]() , не удалось и поэтому попытаемся
реализовать процедуру постепенного подбора. Для этого нужно ввести некоторый
критерий, по которому можно было бы определять в каких точках следует изменить
коэффициент регуляризации. Известно, что кривая ЭДС для импульса-ступеньки
является не возрастающей. Используем это. Пусть, изначально
, не удалось и поэтому попытаемся
реализовать процедуру постепенного подбора. Для этого нужно ввести некоторый
критерий, по которому можно было бы определять в каких точках следует изменить
коэффициент регуляризации. Известно, что кривая ЭДС для импульса-ступеньки
является не возрастающей. Используем это. Пусть, изначально ![]() имеют некоторое малое значение (пока что
одинаковое для всех i). Решаем систему (5.2).
Если полученное решение не монотонно, то в точке, где ЭДС начинает возрастать
увеличиваем коэффициент и снова решаем систему (5.2). Если монотонность не
достигнута, снова увеличиваем
имеют некоторое малое значение (пока что
одинаковое для всех i). Решаем систему (5.2).
Если полученное решение не монотонно, то в точке, где ЭДС начинает возрастать
увеличиваем коэффициент и снова решаем систему (5.2). Если монотонность не
достигнута, снова увеличиваем ![]() и т.д. Реально нет
смысла увеличивать отдельные коэффициенты. Вообще, желательно чтобы
и т.д. Реально нет
смысла увеличивать отдельные коэффициенты. Вообще, желательно чтобы ![]() не убывали, так как в противном случае, в
тех местах где коэффициенты убывают, учитывая то что ЭДС не возрастает, имеется
потенциальная возможность появления колебаний в решении. В связи с этим, как
только обнаружили некорректную точку (пусть она имеет номер s), увеличиваем коэффициенты начиная с
не убывали, так как в противном случае, в
тех местах где коэффициенты убывают, учитывая то что ЭДС не возрастает, имеется
потенциальная возможность появления колебаний в решении. В связи с этим, как
только обнаружили некорректную точку (пусть она имеет номер s), увеличиваем коэффициенты начиная с ![]() и далее, пока не восстановится
монотонность (хотя бы нестрогая). Так как, изначально все коэффициенты были
одинаковые и, следовательно, имела место нестрогая монотонность, то чтобы ее
восстановить, в худшем случае придется увеличить
и далее, пока не восстановится
монотонность (хотя бы нестрогая). Так как, изначально все коэффициенты были
одинаковые и, следовательно, имела место нестрогая монотонность, то чтобы ее
восстановить, в худшем случае придется увеличить ![]() .
.
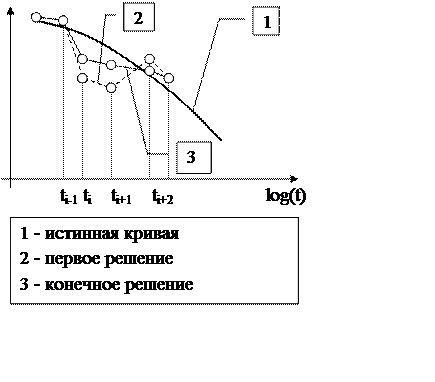 |
Рис.5.1 Схематичный вид решения, при использовании регуляризации.
Алгоритм обнаруживает возрастание в точке ![]() и увеличивает
и увеличивает ![]() ,
разность
,
разность ![]() уменьшается, но с другой стороны,
уменьшается, но с другой стороны, ![]() остался тем же и
остался тем же и ![]() практически
не меняется, таким образом конечное решение будет лежать ниже истинного. Лучшим
вариантом было бы увеличить и коэффициент
практически
не меняется, таким образом конечное решение будет лежать ниже истинного. Лучшим
вариантом было бы увеличить и коэффициент ![]() , и
, и ![]() . С этой целью был введен контроль за
изменением производной: если в некоторой точке производная резко изменилась по
отношению к производной в предыдущей точке, то увеличивается коэффициент,
соответствующий большей производной. Этот метод по сравнению с предыдущим дает
лучшие результаты, хотя в ряде случаев все равно полученное решение, лежит
ниже истинного. Построить критерий, который бы показывал, что в некоторой точке
коэффициент слишком велик не удалось, поэтому остается только подбирать
. С этой целью был введен контроль за
изменением производной: если в некоторой точке производная резко изменилась по
отношению к производной в предыдущей точке, то увеличивается коэффициент,
соответствующий большей производной. Этот метод по сравнению с предыдущим дает
лучшие результаты, хотя в ряде случаев все равно полученное решение, лежит
ниже истинного. Построить критерий, который бы показывал, что в некоторой точке
коэффициент слишком велик не удалось, поэтому остается только подбирать ![]() плавно двигаясь снизу вверх и главное не
перестараться. В связи с этим не стоит сразу требовать монотонности:
тестирование показало, что лучше разрешить малое возрастание (скажем 1%-5%),
тогда получается решение, плавно колеблющееся около истинного, а не лежащее под
ним, как это было в предыдущем случае.
плавно двигаясь снизу вверх и главное не
перестараться. В связи с этим не стоит сразу требовать монотонности:
тестирование показало, что лучше разрешить малое возрастание (скажем 1%-5%),
тогда получается решение, плавно колеблющееся около истинного, а не лежащее под
ним, как это было в предыдущем случае.
В итоге был реализован следующий подход: проводим регуляризацию, по описанному выше алгоритму и разрешаем малое возрастание, после этого сглаживаем полученное решение с условием, что сглаживающий сплайн должен быть монотонным (если сплайн получился немонотонный, то увеличиваем подинтервал сглаживания, на котором нарушилась монотонность). Сглаженную кривую используем для подбора среды в программном комплексе HORIZON. Сглаживание выполняется по двум причинам, во-первых желательно чтобы кривая была монотонной, во-вторых на гладкой кривой лучше работает процедура подбора горизонтально-слоистой среды.
Рассмотрим построение сглаживающего сплайна [3].
Пусть имеется n значений
![]() , нужно построить кубический полином
, нужно построить кубический полином ![]() , такой, что
, такой, что 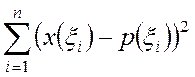 будет
минимальной. Используем кубические базисные функции
будет
минимальной. Используем кубические базисные функции ![]() ,
которые были описаны выше (см. п.3.2.2), тогда
,
которые были описаны выше (см. п.3.2.2), тогда
![]() .
.
Коэффициенты ![]() ищутся из условия минимизации суммы
квадратов отклонений:
ищутся из условия минимизации суммы
квадратов отклонений:
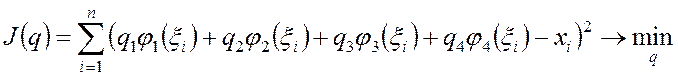
Продифференцируем функционал
по ![]() и приравняем производные к нулю:
и приравняем производные к нулю:
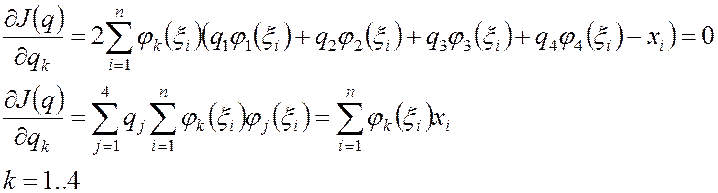
Матрицу для этой системы
удобно получать суммированием локальных матриц, соответствующих точкам ![]() :
:
![]() (5.3)
(5.3)
Как построить сплайн на произвольном интервале было рассмотрено в п.3.2.2.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.