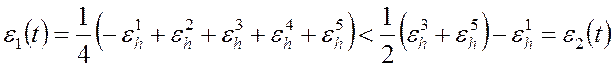Разложение импульса.Разложение ЭДС.Использование регуляризации, страница 3

, то есть на грубой сетке значение исходной ЭДС будет завышенным или, что то же самое, при решении обратной задачи ЭДС для импульса-ступеньки окажется заниженной. Естественно, что при более подробном разложении импульса, мы получаем более точные значения ЭДС. Однако если добавление узла  дает ощутимое улучшение, то добавление  практически ничего не меняет. Принимая во внимание все выше сказанное, можно сделать вывод, что имеет смысл сгущать сетку ближе к концу импульса. Для этой цели предусмотрен специальный коэффициент сгущения. Он задает изменение  (мелкости разбиения) после того, как будет поставлен очередной узел, то есть на каждом шаге  вычисляется как , где  - коэффициент сгущения. Заметим, что, так как разложение импульса выгодней начинать с конца, то  должен быть больше единицы, а  определяет самый маленький шаг (первый с конца).

3.  Разложение ЭДС

3.1.  Представление исходной ЭДС в виде суммы ЭДС для импульсов-ступенек

Покажем, что если импульс представлен в виде суммы импульсов-ступенек, то соответствующая ему ЭДС будет представима в виде

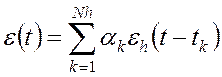,                                 (3.1)

где - берутся из разложения (2.4), - исходная ЭДС,  - ЭДС для импульса в виде функции-ступеньки (далее просто ЭДС для импульса-ступеньки).

Фундаментальной математической моделью в задачах электродинамики является система уравнений Максвелла, устанавливающая аналитическую связь в форме системы векторных дифференциальных уравнений между компонентами электрического и магнитного полей, параметрами среды (электропроводностью, магнитной и диэлектрической проницаемостью) и сторонними возбудителями поля. Мы будем использовать систему уравнений Максвелла в виде:

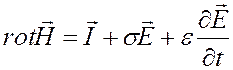,                                (3.2)

,

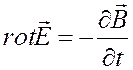, где  – напряженность магнитного поля,  – вектор плотностей сторонних токов (возбуждающих электромагнитное поле),  – напряженность электрического поля, s – проводимость среды, e – диэлектрическая проницаемость среды,  – индукция магнитного поля (связанная с напряженностью  соотношением , где m  – коэффициент магнитной проницаемости, в нашем случае будем считать его постоянным и равным магнитной проницаемости вакуума m₀). Последнее слагаемое в (3.2) будет давать ощутимый вклад только на очень ранних временах (порядка 10-100нс). В рассматриваемой задаче такие времена не задействованы, поэтому в дальнейшем будем пренебрегать этим слагаемым.

Введем вектор-потенциал  с помощью соотношений [11]

,

.

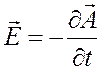В этом случае система уравнений Максвелла преобразуется к виду

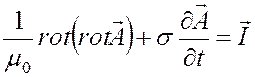.                              (3.3)

Так как в нашем случае электромагнитное поле возбуждается круговой петлей с током, лежащей в горизонтальной плоскости, то вектор плотностей сторонних токов будет иметь только одну ненулевую компоненту:  и (3.3) можно переписать в виде

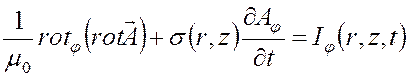,                 (3.4)

где .

В цилиндрической системе координат для вектор-потенциала  справедливы следующие отношения

,

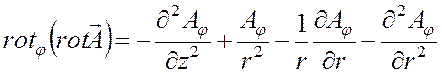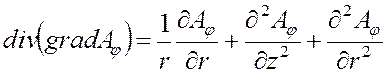, поэтому уравнение (3.4) примет вид

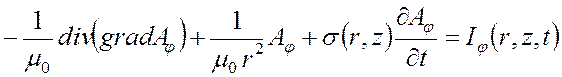.     (3.5)

Пусть имеем два импульса  и  и решаем для них уравнение (3.5):

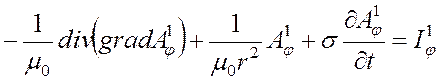 ,              (3.6)

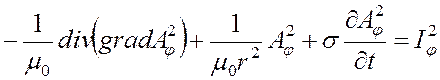.               (3.7)

Легко видеть, что для суммы  импульсов  решение будет иметь вид , для этого достаточно сложить уравнения (3.6)-(3.7) и воспользоваться свойством линейности оператора дифференцирования:

.

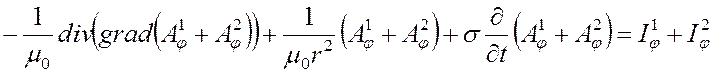Пусть теперь  и  связаны соотношением . Подставляя это в (3.7) и делая замену переменной , получаем

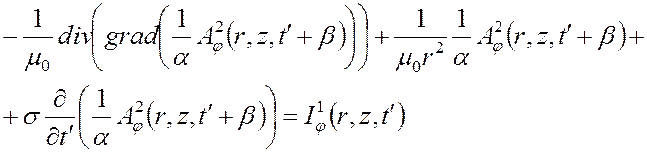
Сравнивая это уравнение с (3.6), получаем

.

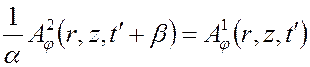Возвращаясь к старой переменной имеем

.

Мы показали, что для импульса, представленного в виде , решение уравнения (3.5) имеет вид . Очевидно, что это будет справедливо для любого количества слагаемых. Теперь нужно перейти от  к ЭДС и убедиться, что все выше сказанной останется справедливым и для ЭДС. Чтобы найти ЭДС, нужно сначала получить индукцию магнитного поля

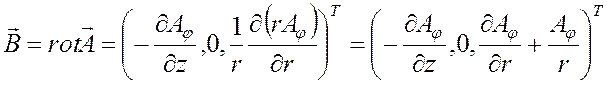, (3.8)

а затем проинтегрировать ее по поверхности приемника (в нашем случае приемник - это круговая петля, расположенная в горизонтальной плоскости, поэтому при вычислении ЭДС используется только z-компонента вектора )

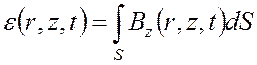.                              (3.9)