Рис.4.8 Результаты восстановления для четвертьсинуса. Показаны относительные отклонения от ЭДС для импульса-ступеньки из пакета HORIZON
Рис.4.9 Результаты восстановления для полусинуса
Ошибка для четвертьсинуса (рис.4.8) относительно уже имеющейся остается, в общем, в пределах 5% (такой же был и уровень шума). А вот для полусинуса, полученное решение вряд ли можно считать хоть каким-то результатом (см. рис.4.9).
В следующих тестах, исходная ЭДС возмущается путем умножения на некоторую кривую, задающую относительное отклонение от истинного значения. В данном случае шум выглядит, как показано на рис.4.10.
Рис.4.10 Относительное отклонение возмущенных кривых ЭДС от истинной
Рис.4.11 Относительное отклонение восстановленных кривых от истинной
Приведенные тесты показывают, что к низкочастотным возмущениям метод безразличен, но вот с увеличением частоты возмущающего воздействия, в решении начинают появляться непропорциональные осцилляции.
Сравнивая матрицы СЛАУ построенные при восстановлении ЭДС, можно заметить, что матрица в случае с полусинусом имеет на диагонали элементы, которые значительно меньше вне диагональных элементов в соответствующей строке. Такая разнородность элементов частично обусловлена неравномерным шагом по времени. Если возмущающее воздействие было низкочастотным, то есть изменялось достаточно плавно, то с учетом того, что сумма элементов по строке равна нулю, ошибки успевают компенсировать друг друга и не накапливаются. Если же имеем высокочастотный шум, то ошибки ведут себя хаотически и уже не могут скомпенсировать друг друга.
В матрице для четвертьсинуса диагональный элемент
всегда больше либо равен вне диагональным, поэтому ошибка не увеличивается. На
диагональ всегда попадает последний коэффициент 
(или
сумма нескольких последних) из разложения (2.4) и, если импульс в конце резко
изменяется до нуля (как в случае с четвертьсинусом), то этот коэффициент будет
большим. Полусинус же подходит к нулю плавно и последний коэффициент разложения
достаточно мал.
Так как описанный метод восстановления ЭДС для импульса-ступеньки оказался неустойчивым, а на практике исходная ЭДС всегда будет содержать шум, то для восстановления ЭДС будем использовать процедуру регуляризации при решении СЛАУ.
Решение системы линейных уравнений 
эквивалентно минимизации функционала 
. Добавим в функционал еще одно слагаемое:
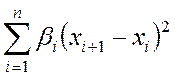. (5.1)
Теперь при минимизации функционала не просто решается система уравнений, но и требуется еще, чтобы разница между соседними компонентами решения была ограничена (фактически ограничиваем производную решения).
По рис.4.9 видно, что решение исходной системы имеет
очень большие колебания, поэтому имеет смысл выбрать регуляризирующую добавку
вида (5.1), причем вместо 
возьмем
конечно-разностную производную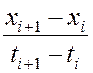 
(это обусловлено тем,
что для кривых ЭДС шаг по времени сильно неравномерный). В нашем случае вместо 
будут 
.
Получим матрицу новой регуляризированной системы, для этого продифференцируем
функционал 
по и
приравняем производные к нулю.
.
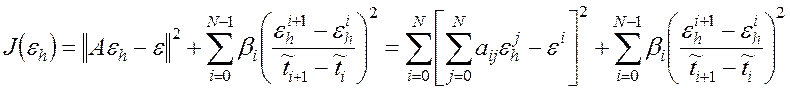
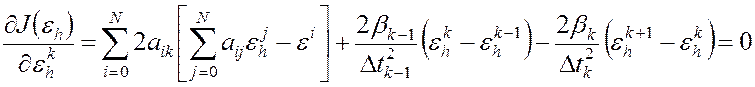
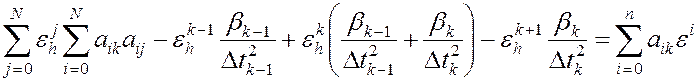
Первое и последнее уравнения получаются аналогично. Напомним, что N - это количество точек, в которых задана исходная ЭДС, а система имеет размерность N+1 (см. п.3.2).
В матричной форме:
, (5.2)
где
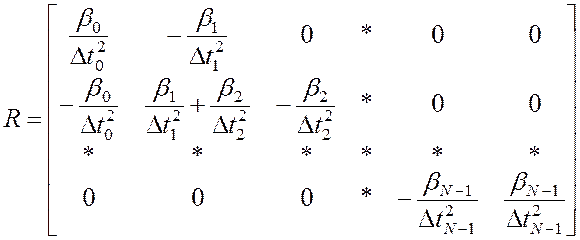
Система (5.2) имеет симметричную положительно полуопределенную матрицу, решаем методом Холецкого [3,10].
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
