Разложение импульса.Разложение ЭДС.Использование регуляризации, страница 4

Из соотношений (3.8) и (3.9) очевидно, что для импульса, имеющего вид (2.4), ЭДС будет представляться в виде (3.1).

3.2.  Построение дискретного аналога ЭДС для импульса-ступеньки

Вернемся к вопросу нахождения ЭДС для импульса-ступеньки. Исходная ЭДС задана в виде дискретного набора точек . Расписывая (3.1) для каждой такой точки получим систему из N уравнений. Неизвестными являются значения , которые и надо определить, только их пока больше чем уравнений, поэтому для  придется построить сетку и искать значения ЭДС для импульса-ступеньки в узлах, используя некоторую аппроксимацию. Надо отметить, что сетка не может быть произвольной, так как в этом случае возможно получение вырожденной СЛАУ. Покажем это на примере. Пусть задана некоторая сетка (см. рис.3.1) и пусть нам известны значения исходной ЭДС в точках  и , а длина импульса равна . Тогда значение  выразится через значения , лежащие в интервале , аналогично  — через . В результате, узел  не войдет ни в одно уравнение и матрица СЛАУ будет не полного ранга.

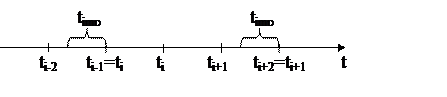Рис.3.1 Некорректная сетка для ЭДС для импульса-ступеньки

Чтобы матрица СЛАУ была невырожденной, расположим узлы в точках , где  - времена, в которых заданы значения исходной ЭДС,  - длина импульса.

.

Такое расположение узлов гарантирует отсутствие нулевых элементов на главной диагонали матрицы. Само по себе это еще не гарантирует невырожденности системы, но в дальнейшем будет видно, что СЛАУ построенная для такой сетки действительно является невырожденной.

Обратим внимание, что если среди  имеются такие, что лежат левее , то в сетке появятся узлы, лежащие в отрицательной области. Так как  при  не определена, то толку от таких узлов нет, поэтому перед построением сетки мы удаляем все .

При построении сетки указанным выше способом, возникает проблема с последним узлом, который будет расположен в точке  ( - это последняя точка, в которой известна исходная ЭДС). Исходная ЭДС представляется в этой точке следующим образом:

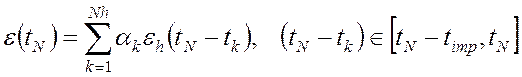, то есть, нужны значения , лежащие за последним узлом сетки и пока не входящие в СЛАУ. Чтобы исправить это положение, достаточно добавить еще один узел: . Но теперь, неизвестных на одну больше, чем уравнений. Проэкстраполируем  в точку , для этого воспользуемся формулой, дающей асимптотическое поведение ЭДС для импульса-ступеньки для больших времен [4,17]:

, где k - коэффициент, зависящий от среды.

Коэффициент k определим по значению  в предыдущем узле:

.

Таким образом, дополнительное уравнение будет иметь вид:

.                    (3.10)

На настоящий момент остается только определиться, как аппроксимировать  на отрезках  и можно переходить к построению СЛАУ. В данной работе будут рассмотрены два вида аппроксимации: линейная и сплайновая.

3.2.1.  Линейная аппроксимация ЭДС

Рассмотрим сначала линейную аппроксимацию. Будем считать, что на каждом интервале  функция  изменяется линейно от значения в точке  до значения в . Введем для удобства локальную нумерацию так, что узел  получит номер один , узел  — номер два . Используя локальные кусочно-линейные базисные функции можно записать:

,                (3.11)

где  - значения ЭДС для импульса-ступеньки в узлах,  - локальные кусочно-линейные базисные функции, имеющие вид

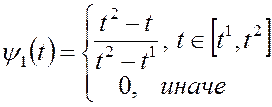
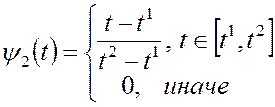
СЛАУ получается следующим образом: для каждой точки , в которой задано значение исходной ЭДС, выписываем представление (3.1), причем, если значения  попадают между узлами, то используем линейную аппроксимацию (3.11), в конце записываем дополнительное уравнение (3.10).

Легко видеть, что для сетки, построенной описанным выше способом и линейной аппроксимации, матрица СЛАУ будет иметь верхнетреугольный вид за исключением последней строки, соответствующей уравнению (3.10), в которой находятся кроме диагонального, еще один ненулевой элемент.

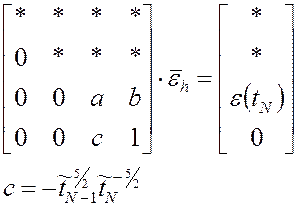
Проведем исключение элемента c, для этого домножим первую и вторую строки снизу на -с и a соответственно,  а затем сложим их:

, где  - значение ЭДС для импульса-ступеньки в N-ом узле (здесь нумерация глобальная).