Разложение импульса.Разложение ЭДС.Использование регуляризации, страница 2

Возможно, конечно, решать прямую задачу используя универсальный метод решения дифференциальных уравнений в частных производных — метод конечных элементов [5,7,11-13], но применение стандартных конечноэлементных схем не приводит к быстрым алгоритмам вычисления интересующих характеристик электромагнитного поля в горизонтально-слоистой среде. Так как, в рассматриваемой ситуации, главной целью является все же решение обратной задачи, то из-за низкой скорости применение таких схем нежелательно.

В данной работе предлагается простой способ преобразования имеющейся ЭДС к ЭДС, которая соответствовала бы той же самой среде, что и исходная, но при мгновенном выключении тока в петле генератора. Преобразование основано на представлении имеющегося импульса в виде суммы импульсов-ступенек, которые удовлетворяют упомянутой выше модели.

2.  Разложение импульса

2.1.  Представление импульса в виде суммы импульсов-ступенек

Для того чтобы выполнить преобразование ЭДС, представим импульс в виде суммы импульсов-ступенек.

Пусть импульс определен на временно'м интервале , при  и  будем считать, что . Нанесем на этот интервал сетку с узлами , такую что . На каждом отрезке  будем аппроксимировать функцию  кусочно-постоянными базисными функциями, тогда

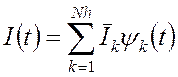,                                     (2.1)

где - усредненное значение импульса на k-ом отрезке, - кусочно-постоянная базисная функция:

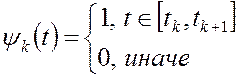
Теперь нужно перейти от кусочно-постоянных базисных функций к функциям-ступенькам:

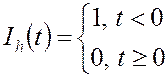
Разница в том, что  на интервалах левее k-ко равна нулю, а  - единице. Выразим  через :

Подставим в представление (2.1):

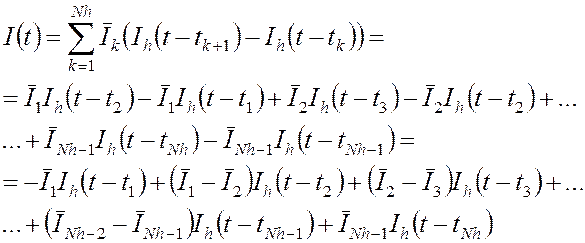   (2.2)

Введем обозначения

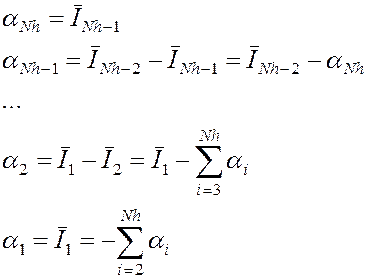                     (2.3)

тогда (2.2) запишется в виде

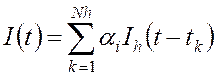                                  (2.4)

Коэффициенты разложения  можно найти из системы (2.3). Матрица для этой системы имеет верхнетреугольный вид, таким образом, если рассматривать отрезки в обратном порядке , то можно найти коэффициенты не составляя СЛАУ.

Значения  будем выбирать из условия

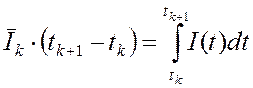,                              (2.5)

то есть на отрезке , интегральный ток исходного импульса должен совпадать с интегральным током импульса-ступеньки. Интеграл будем вычислять пологая, что  линейна на отрезке :

.

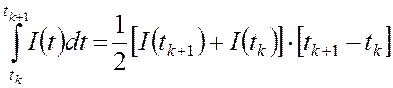Аппроксимировать  при вычислении интеграла с более высоким порядком не имеет смысла, так как разложение по кусочно-постоянным базисным функциям все равно будет давать бо'льшую ошибку.

2.2.  Построение сетки при разложении импульса

В предыдущем пункте было показано, как получить разложение импульса по функциям-ступенькам, при этом область, в которой проводилось разложение, покрывалась некоторой сеткой. Рассмотрим построение этой сетки. Первый и последний узлы ставятся на границах  и  соответственно. Внутренние узлы  ставятся в точках, в которых выполняется соотношение , то есть когда относительное изменение импульса будет равно  (далее этот параметр будем называть мелкостью разбиения). Такой подход обеспечит сгущение сетки в местах, где  имеет большую производную, и разрежение там, где производная мала.

Далее будет показано, что если импульс представлен в виде (2.4), то соответствующая ему ЭДС также распадется на сумму:

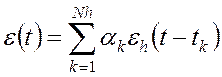.                                 (2.5)

Зная как представляется исходная ЭДС, рассмотрим две сетки:  и  (см. рис.2.1) и найдем значение ЭДС в точке , лежащей близко к . Выпишем соотношение (2.5) для этих сеток:

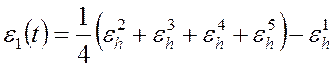,                        (2.6)

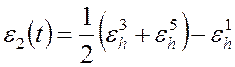.                                (2.7)

Рис.2.1 Представление импульса в виде суммы импульсов-ступенек и соответствующие им ЭДС без учета коэффициентов

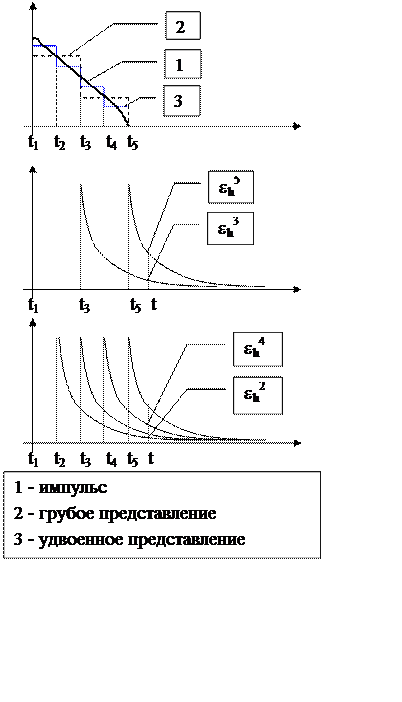Так как ЭДС очень быстро убывает на ранних временах, то  и . С другой стороны, при больших , ЭДС изменяется достаточно плавно и . Подставляя в (2.6) и, учитывая (2.7), получаем