Проектирование алгоритма управления электрогидравлическим приводом», страница 9

9.3392e-001+ 3.5765e-001i 9.3392e-001- 3.5765e-001i 5.7407e-002             

9.3352e-001+ 3.6507e-001i 9.3352e-001- 3.6507e-001i 5.6757e-002

Принимаем: Kr=0.23

После того, как мы определили Кr, Необходимо проверить качество переходных процессов в замкнутой системе с пропорциональным регулятором и ее точность.

Качество переходного процесса оценивается по реакциям системы на ступенчатое изменение задающего воздействия. Передаточная функция замкнутой системы к задающему воздействию, приложенному на входе регулятора, имеет вид

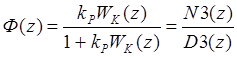
Полиномы МЗ и D3 связаны с полиномами М и D передаточной функции Wk(z) соотношениями

N3=Кr*N1

D3=D1+Kr*N1

Реакция на ступенчатое воздействие вычисляется с помощью функции DSTEP:

Y=DSTEP(N3, D3, L)

L - число точек (периодов квантования)

Y=dstep(M3,D3,200)

При К=0,23 процесс получается очень колебательным, поэтому уменьшаем К.

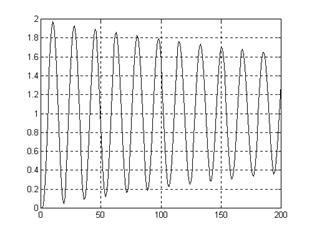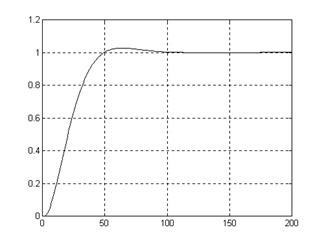К=0,01

В данном случае нас удовлетворяет форма переходного процесса, но велика его длительность. Произведем оценку системы на точность.

Точность следящей системы оценивается по величине амплитуды установившейся ошибке при отработке синусоидального задающего воздействия. Параметры задающего воздействия (частота и амплитуда) определены в задании. Передаточная функция следящей системы Фq , связывающая ошибку с задающим воздействием, находится по формуле:

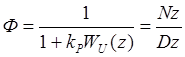
В нашем случае: Nz=D1  Dz=D1+kr*N1.

Для определения реакции системы нужно предварительно сформировать входное воздействие длительностью L периодов квантования, которая на (0,5-1,5) периодов синусоиды должна превышать определенное выше время переходного процесса:

I=0:1:600

UV=Ag*sin(wg*t0*l)

График ошибки находится с помощью функции DLSIM:

TET=DLSIM(Nz, Dz, UV)

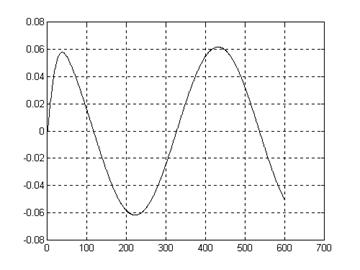max(TET)= 0.06, q_доп=0.005, max(TET)>>q_доп

Cистема не удовлетворяет заданным условиям. Требуется дополнительная коррекция.

2III.4 Синтез цифрового управления

Алгоритм управления, реализуемый в цифровом регуляторе, должен быть выбран таким образом, чтобы система удовлетворяла требованиям задания на проектирование Расчет алгоритма управления (иначе - алгоритм коррекции или закон управления) выполняется методом логарифмических частотных характеристик. Расчетная схема системы представлена на рис. 4,1.

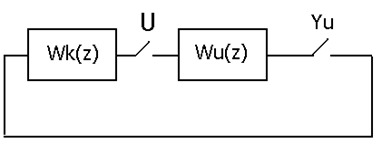
Рис.4.1

На рис 4.1 W_К(z) обозначена передаточная функция, описывающая алгоритм управления , которую надлежит определить.

Идея метода логарифмических частотных характеристик (ЛЧХ) состоит в приведении передаточной функции разомкнутой системы W(z)=W_k(z)*W_u(z) к виду некой желаемой передаточной функции W_ж(z), т.е. в обеспечении условия W(z)=W_ж(z). Желаемая передаточная функция выбирается исходя из требований к системе. Расчеты выполняются графоаналитическим методом с использованием логарифмических характеристик, построенных в функции псевдочастоты lср. Для получения характеристик известной передаточной функции, например W_u(z), необходимо перейти от z-преобразования к w-преобразованию, а затем сделать замену w=jl. Этот переход выполняется с помощью функции Z2W

[Aa, Bb]=z2w(N1,D1,T0)

в результате применения которой находится передаточная функция:

NW(jl)

W_u(jl) = ------------DW(jl)

1.788300648088079e+003      -5.731657400709677e+002

Aa = 6.666666666666669e+002 Bb = -4.078741170560915e+001

-8.518917889264113e+002      1.332267629550219e-012

Переход к форме типовых звеньев

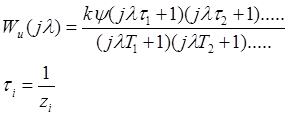      (4.1)

Далее, приступаем к построению ЖЛЧХ. ЖЛЧХ должна проходить выше критической точки с абсциссой Igw_b и ординатой

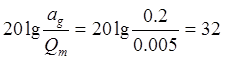
для следящей системы. Формально это единственное требование к низкочастотной части ЖЛЧХ.

Среднечастотная часть ЖЛЧХ формируется на основании требований к переходным процессам в системе, причем учитываются два основных показателя: длительность переходного процесса (время регулирования) t_p и перерегулирования s. Заданное время регулирование обеспечивается выполнением неравенства

l_с - частота среза ЖЛЧХ.